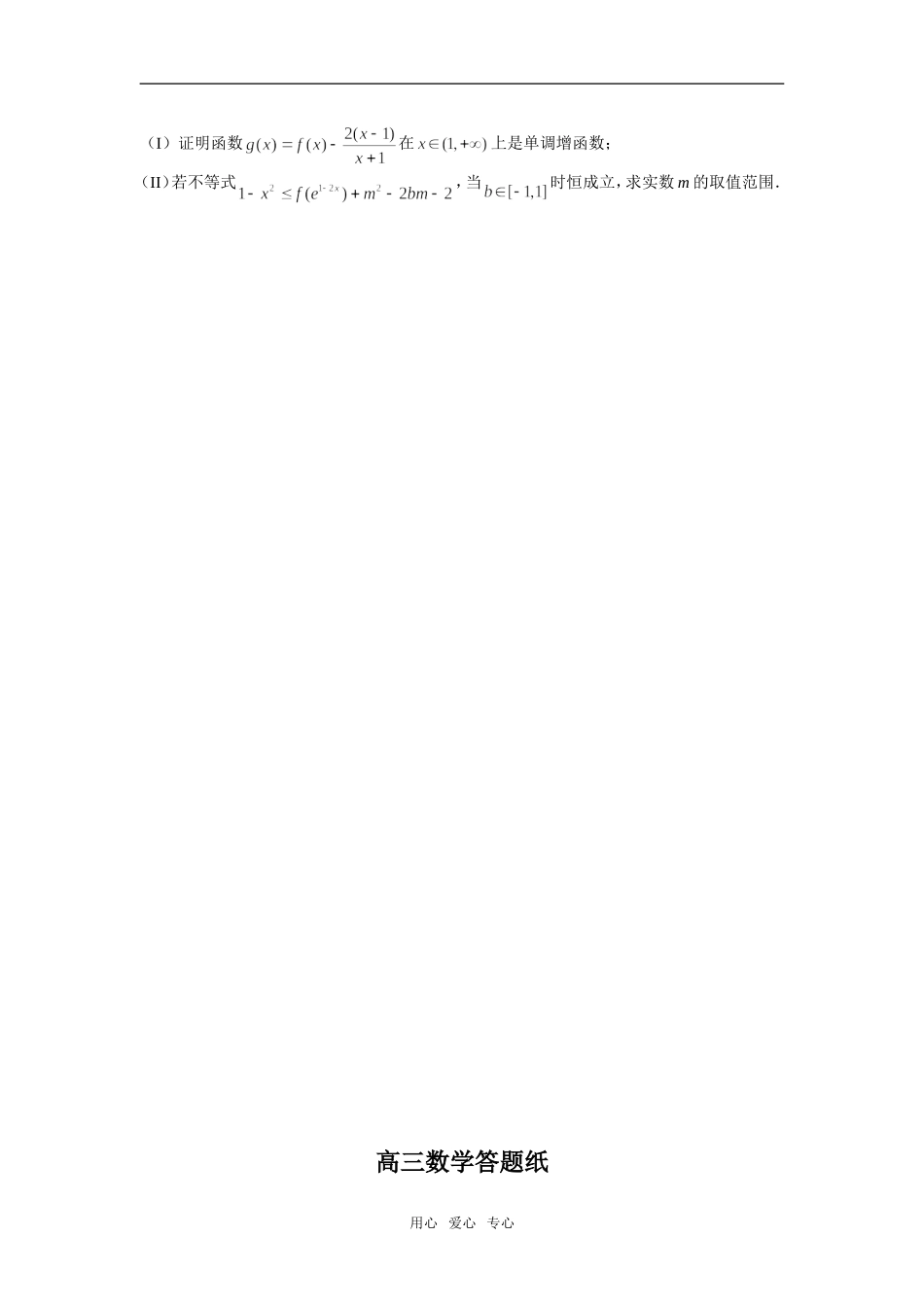
江苏扬州树人中学高三测试1一.填空题:1.设集合A={-2,-1,1,2,3},B={x|x2>3},则A∩B=__________________2.已知向量a=(x,3),b=(-2,1)平行,则实数x=_________________3.如果cos=-,∈(,),那么cos(+)的值等于_________________4.设点P是函数的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值,则ω=5.由正数构成的等比数列{an},若,则.6.若方程的解为,则不小于的最小整数是7.已知函数f(x)是奇函数,当x<0时,f(x)=x2-3asin,且f(3)=6,则a=________8.如图,函数的图象在点P处的切线是,则=.9.已知,则的值=10.已知函数的图象(部分)如图所示,则的解析式为=11.已知,,且,则向量与向量的夹角是12.如果关于的方程在上有解,求的取值范围是13.已知p:不等式|x–1|+|x+2|>m的解集为R,q:f(x)=log5–2mx为减函数,则p是q成立的条件用心爱心专心424.5xyO(第8题图)y=f(x)l14.定义在(-∞,+∞)上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上是增函数,下面是关于f(x)的判断:①f(x)是周期函数;②f(x)的图像关于直线x=1对称;③f(x)在[0,1]上是增函数;④f(2)=f(0).其中正确的判断是_____________________(把你认为正确的判断都填上)二.解答题:15.设函数f(x)=a·b,其中向量a=(cosx+1,),b=(cosx-1,2sinx),x∈R.(Ⅰ)求f(x)的最小正周期T;(Ⅱ)函数f(x)的图像是由函数f(x)=sinx的图像通过怎样的伸缩或平移变换后得到的?16.设是定义在上的单调增函数,满足,.求:(1)f(1)(2)若,求x的取值范围。17.在中,,.(Ⅰ)求角的大小;(Ⅱ)若最大边的边长为,求最小边的边长.18.设是公比大于1的等比数列,为数列的前项和.已知,且构成等差数列.(1)求数列的通项公式.(2)令求数列的前项和.19.已知数列的前项和为,点在直线上,其中.令,且,(1)求数列的通项公式;(2)若,求的表达式,并比较与的大小.20.设函数用心爱心专心(I)证明函数在上是单调增函数;(II)若不等式,当时恒成立,求实数m的取值范围.高三数学答题纸用心爱心专心一.填空题(每题5分,共70分)1.{-2,2,3}2.-63.-4.25.76.57.58.9/89-7/510.11.12.13.必要不充分14.①②④二.解答题(15、16题每题14分,17、18题每题15分,19、20题每题16分)15题:解:(Ⅰ)依题设f(x)=2cos2x-1+23sinxcosx==2sin(2x+6).∴(Ⅱ)函数y=sinx的图象通过如下的变换:①将函数f(x)=sinx上所有的点向左平移6个单位长度,得到函数f(x)=sin(x+6)的图象;②将函数f(x)=sin(x+6)上所有的点的横坐标缩短到原来的倍,纵坐标不变,得到函数f(x)=sin(2x+6)的图象;③将函数f(x)=sin(2x+6)上所有的点的纵坐标伸长到原来的2倍,横坐标不变,得到函数f(x)=2sin(2x+6)的图象.16题:解:(1)(2),从而有即是上的增函数,故用心爱心专心解之得:17题:解:(Ⅰ),.又,.(Ⅱ),边最大,即.又,角最小,边为最小边.由且,得.由得:.所以,最小边.18题:解:(1)由已知得解得.用心爱心专心设数列的公比为,由,可得.又,可知,即,解得.由题意得..故数列的通项为.(2)由于由(1)得又是等差数列.故.用心爱心专心19题:解:(1) ,∴.∴().∴().∴().∴().∴数列为等比数列,其公比为,首项,而,且,∴.∴.∴.(2) ,∴.∴.∴,①∴2.②①-②得-,,∴.∴()==.当时,=;用心爱心专心当时,-()=4(4-5)=-4,;当时,,且,∴时,总有.∴时,总有20题:(I),当时,在上是单调增函数.(II),原不等式即为在时恒成立.的最大值为1,在时恒成立.令,则,且由,解得或由,解得或综上得,或江苏扬州树人中学高三数学测试二一、填空题(每小题5分,计70分)1.函数的定义域为.2.若函数在上是单调函数,则的取值范围是3已知函数,若,则用心爱心专心4.已知A、B是钝角三角形的两个锐角,是偶函数,且在上单调增,则(用“<”、“>”填空)5.f(n+1)=[3f(n)+1],nN*,且f(1)=1,则f(100)的值是6.在等比数列中,,公比q是整数,则=.7.设是偶函数,则的值为8.若的内角满...