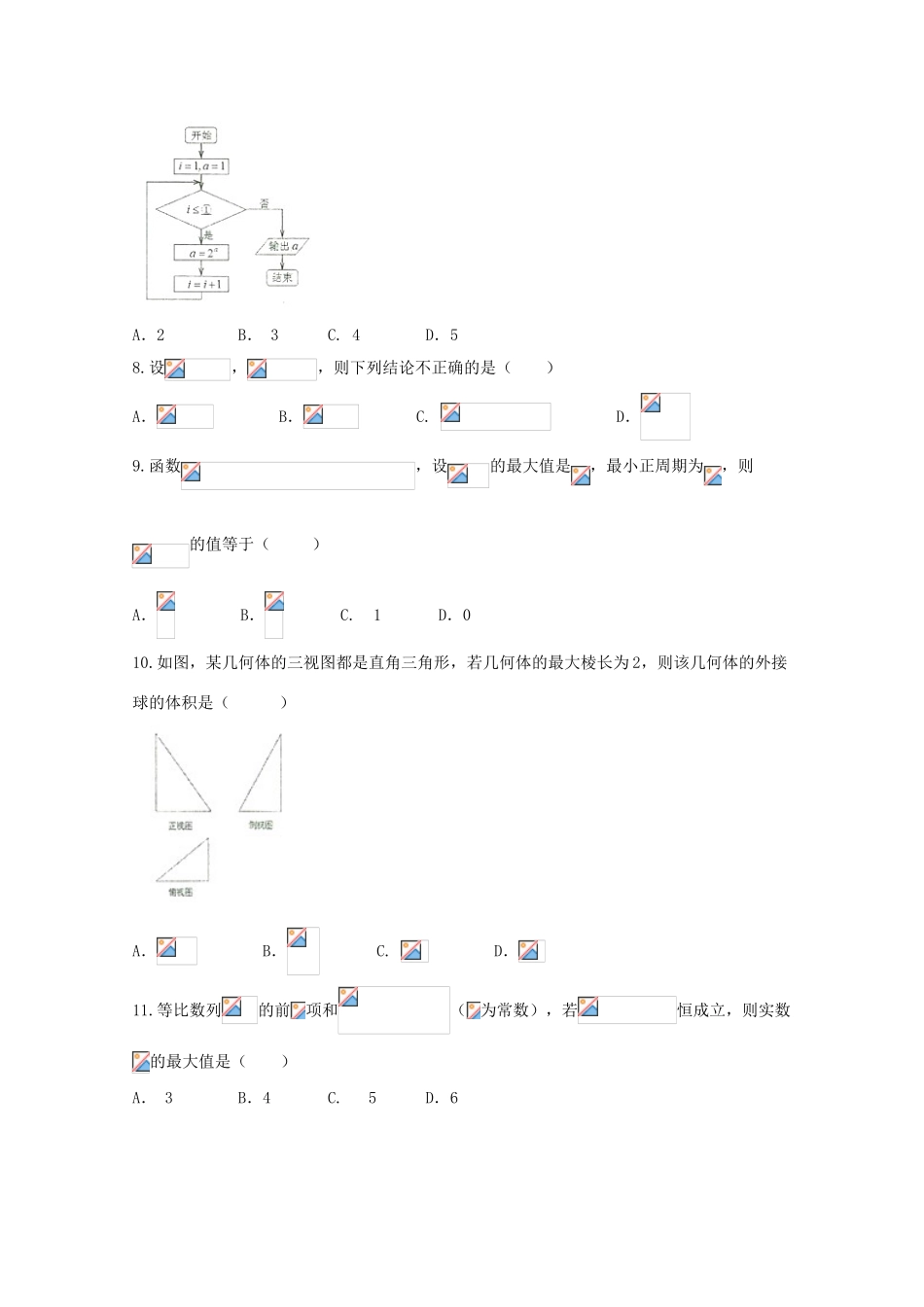
广西陆川县2018届高三数学9月月考试题理第I卷(选择题,共60分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合,,那么()A.B.C.D.2.等差数列满足,,则()A.7B.14C.21D.283.已知,,且,则实数()A.1B.2C.3D.44.设是空间中不同的直线,是不同的平面,则下列说法正确的是()A.,则B.,则C.,则D.,则5.实数满足且,则的最大值为()A.-7B.-1C.5D.76.若,则二项式展开式中的常数项是()A.20B.-20C.-540D.5407.已知流程图如图所示,该程序运行后,若输出的值为16,则循环体的判断框内①处应填()A.2B.3C.4D.58.设,,则下列结论不正确的是()A.B.C.D.9.函数,设的最大值是,最小正周期为,则的值等于()A.B.C.1D.010.如图,某几何体的三视图都是直角三角形,若几何体的最大棱长为2,则该几何体的外接球的体积是()A.B.C.D.11.等比数列的前项和(为常数),若恒成立,则实数的最大值是()A.3B.4C.5D.612.设是双曲线的右顶点,是右焦点,若抛物线的准线上存在一点,使,则双曲线的离心率的范围是()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分)13.若,则的二项展开式中的系数为.14.已知双曲线的左右焦点分别关于两条渐近线的对称点重合,则双曲线的离心率为___________.15.已知锐角三角形中,角所对的边分别为若,则的取值范围是____________.16.已知函数,点为坐标原点,点,向量,是向量与的夹角,则使得恒成立的实数的取值范围为_________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)在中,角、、的对边分别为、、,.(Ⅰ)求角的大小;(Ⅱ)若,,求的值.18.(本小题满分12分)2017年3月智能共享单车项目正式登陆某市,两种车型(“小绿车”、“小黄车”)采用分时段计费的方式,“小绿车”每30分钟收费0.5元(不足30分钟的部分按30分钟计算);“小黄车”每30分钟收费1元(不足30分钟的部分按30分钟计算).有甲、乙、丙三人相互独立的到租车点租车骑行(各租一车一次).设甲、乙、丙不超过30分钟还车的概率分别为,三人租车时间都不会超过60分钟.甲、乙均租用“小绿车”,丙租用“小黄车”.(I)求甲、乙两人所付的费用之和等于丙所付的费用的概率;(Ⅱ)设甲、乙、丙三人所付的费用之和为随机变量,求的分布列和数学期望.19.(本小题满分12分)如图,在四棱锥中,平面,底面是菱形,,.(Ⅰ)求证:;(Ⅱ)若,求二面角的余弦值.20.(本小题满分12分)已知椭圆:(a>b>0)的离心率为,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4.(1)求椭圆的方程;(2)设直线:与椭圆M交于A,B两点,若以AB为直径的圆经过椭圆的右顶点C,求的值.21.(本小题满分12分)PABDC已知函数为自然对数的底数).(1)求F(x)=f(x)-g(x)的单调区间,若F(x)有最值,请求出最值;(2)是否存在正常数,使f(x)与g(x)的图象有且只有一个公共点,且在该公共点处有共同的切线?若存在,求出的值,以及公共点坐标和公切线方程;若不存在,请说明理由.请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题记分.22.(本小题满分10分)《选修4-4:坐标系与参数方程》在直角坐标系中,过点作倾斜角为的直线与曲线相交于不同的两点.(1)写出直线的参数方程;(2)求的取值范围.23.(本小题满分10分)《选修4—5:不等式选讲》已知a+b=1,对,b∈(0,+∞),+≥|2x-1|-|x+1|恒成立,(1)求+的最小值;(2)求的取值范围。理科数学试题参考答案及评分标准一、选择题:1-6:ABCDCC;7-12:BDBBCA13.18014.15.()16.三、解答题17.(本小题满分12分)解:(Ⅰ)由,得........................................3分∴ ,∴...........................................6分(Ⅱ)由正弦定理,得..........................................9分 ,,∴.∴.............................................11分∴............................................12分18.(本小题满分12分)解:(I)由题意得,甲...