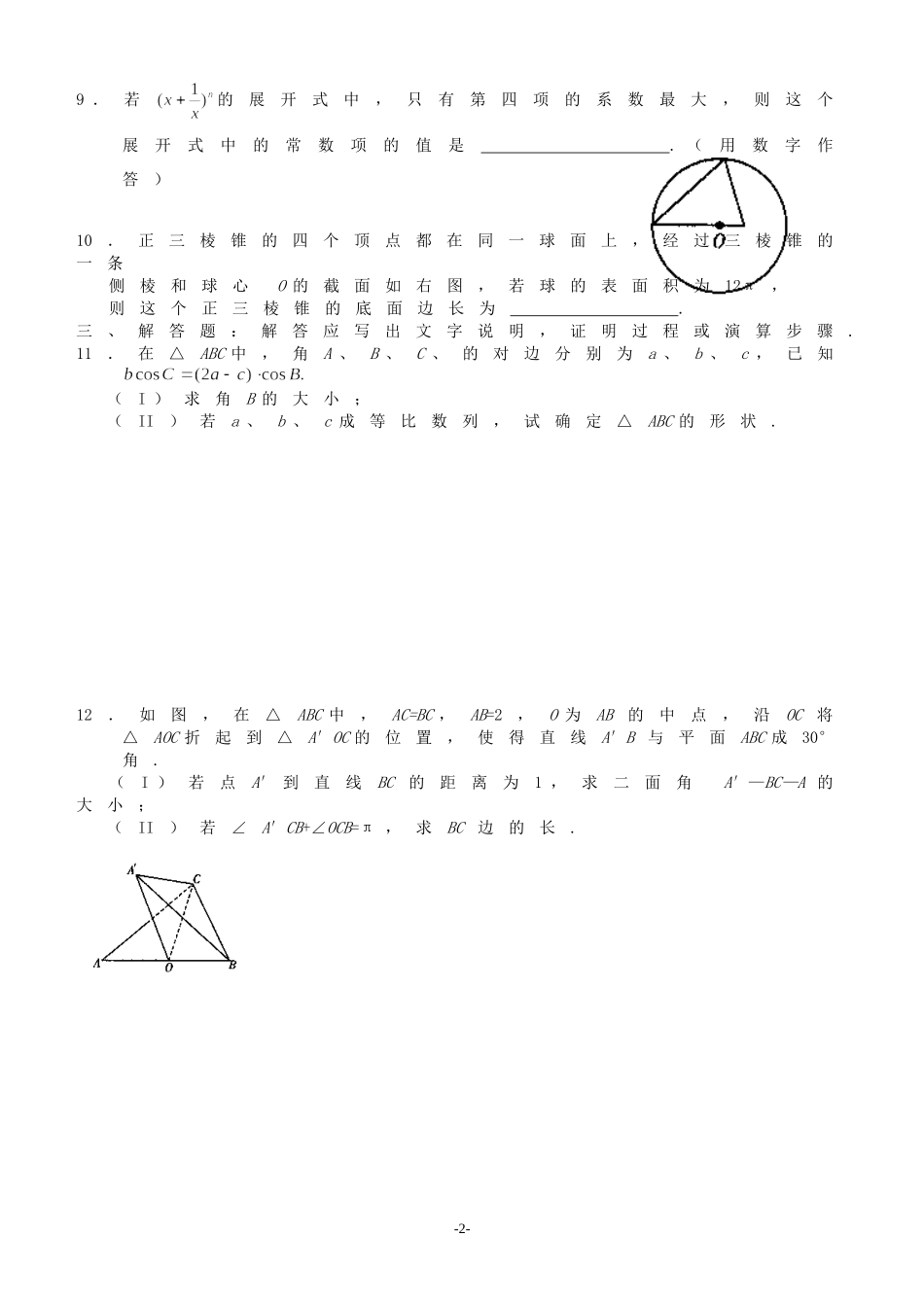
高考数学下学期考前模拟天天练3一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.设l、m为不同的直线,α、β为不同的平面,给出下列四个命题:①若l∥β,m∥β,则α∥β;②若则m⊥β;③若a⊥β,l∥α,则l⊥β;④若α∥β,,则l∥m.其中真命题的个数共有()A.1个B.2个C.3个D.4个2.某两个三口之家,拟乘“富康”、“桑塔纳”两辆出租车一起外出郊游,每辆车最多只能坐4个,其中两个小孩(另4个为两对夫妇)不能独坐一辆车,则不同的乘车方法共有()A.58种B.50种C.48种D.40种3.已知函数是奇函数,则函数的图象关于下列哪个点成中心对称()A.(1,0)B.(-1,0)C.(,0)D.(-,0)4.已知两定点A、B,且|AB|=4,动点P满足|PA|-|PB|=3,则|PA|的最小值是()A.B.C.1D.5.设、、、是半径为2的球面上的四个不同的点,且满足,,,用、、分别表示、、的面积,则的最大值是()A.B.C.D.6.如图,正四面体A—BCD中,点E在棱AB上,点F在棱CD上使得,设与分别表示EF与AC、BD所成的角,则()A.是()上的增函数B.是()上的减函数C.在(0,1)上递增,在()上递减D.是()上的常数函数二、填空题:7.已知,则a与b的大小关系是.8.函数的最小正周期是.--1209.若的展开式中,只有第四项的系数最大,则这个展开式中的常数项的值是.(用数字作答)10.正三棱锥的四个顶点都在同一球面上,经过三棱锥的一条侧棱和球心O的截面如右图,若球的表面积为12π,则这个正三棱锥的底面边长为.三、解答题:解答应写出文字说明,证明过程或演算步骤.11.在△ABC中,角A、B、C、的对边分别为a、b、c,已知(I)求角B的大小;(II)若a、b、c成等比数列,试确定△ABC的形状.12.如图,在△ABC中,AC=BC,AB=2,O为AB的中点,沿OC将△AOC折起到△A′OC的位置,使得直线A′B与平面ABC成30°角.(I)若点A′到直线BC的距离为1,求二面角A′—BC—A的大小;(II)若∠A′CB+∠OCB=π,求BC边的长.--22013.已知数列为等差数列,其前n项和为(I)若成立,并将其整合为一个等式;(II)一般地,若存在正整数k,使,我们可将(I)中的结论作相应推广,试写出推广后的结论,并推断它是否正确.14.设a为实常数,函数(I)若函数的图象在点P(1,)处的切线的倾斜角为,求函数的单调区间;(II)若存在,使,求a的取值范围.--315.已知点A(-1,0),B(1,-1)和抛物线.,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.(I)若△POM的面积为,求向量与的夹角;(II)试探求直线PQ是否过定点?若过定点,求出定点的坐标;若不过定点,说明理由.--4[参考答案]http://www.DearEDU.com一、选择题:1—6:BCCABD二、填空题:7.8.9.2010.3三、解答题:解答应写出文字说明,证明过程或演算步骤.11.解:(I)由已知及正弦定理,有(II)由题设,从而为正三角形.12.解:(I)由已知,OC⊥OB,OC⊥OA′从而平面A′OB⊥平面ABC.过点A′作A′D⊥AB,垂足为D,则A′D⊥平面ABC,∴∠A′ED=30°,又A′O=BO=1,∴∠A′OD=60°,从而A′D=A′Osin60°=.过点D作DE⊥BC,垂足为E,连结A′E,据三垂线定理,A′E⊥BC.∴∠A′ED为二面角A′—BC—A的平面角.由已知,A′E=1,在Rt△A′DE中∴∠A′ED=60°故二面角A′—BC—A的大小为60°.(II)设BC=,∠A′CB=θ,则A′C=,∠OCB=π-θ.在Rt△BOC中,在△A′DB中,A′B=在△A′BC中,A′B2=A′C2+BC2-2A′C·BC13.解:(I)--5;;∴对任意(II)推广:设等差数列的前n项和为Sn,若存在正整数k,使则对任意设的公差为故推广后的结论正确.14.解:(I)据题意,故;故的单调递增区间是[0,],单调递减区间是(-∞,0,[,+∞.(II)(1)若上是减函数。又(2)若从而在(0,上单调递增,在[,+上单调递减.--6据题意,的取值范围是(3,+∞).15.解:(I)设点、M、A三点共线,设∠POM=α,则由此可得tanα=1.又(II)设点、B、Q三点共线,即即由(*)式,代入上式,得由此可知直线PQ过定点E(1,-4).--7