§2.7函数的图象A组基础题组1.(2015北京东城模拟)在同一坐标系中画出函数y=logax,y=ax,y=x+a的图象,可能正确的是()2.(2016领航高考冲刺卷一文,4,5分)函数f(x)=cosx+的大致图象是()3.(2016温州上学期返校联考文,7,5分)函数f(x)=-的图象为()4.(2015浙江冲刺卷五,2)函数y=的图象可能是()5.(2015安徽,9,5分)函数f(x)=的图象如图所示,则下列结论成立的是()A.a>0,b>0,c<0B.a<0,b>0,c>0C.a<0,b>0,c<0D.a<0,b<0,c<06.(2013北京,5,5分)函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)=()A.ex+1B.ex-1C.e-x+1D.e-x-17.(2015海口调研)若当x∈R时,函数f(x)=a|x|(a≠1)始终满足0<|f(x)|≤1,则函数y=loga的图象大致为()8.(2015衢州一模,7,5分)a,b∈R,记max{a,b}=则函数f(x)=max()A.有最大值,无最小值B.有最大值,无最小值C.有最小值,无最大值D.有最小值,无最大值9.(2015浙江镇海中学模拟,8)函数f(x)=的图象上关于原点对称的点有()A.0对B.2对C.3对D.无数对10.(2015衢州一模,17,4分)已知x∈R,[x]表示不超过x的最大整数,若函数f(x)=-a(x≠0)有且仅有3个零点,则实数a的取值范围是.11.已知函数f(x)=|x2-4x+3|.(1)求函数f(x)的单调区间,并指出其增减性;(2)求集合M={m|使方程f(x)=m有四个不相等的实根}.B组提升题组1.(2014山东,6,5分)已知函数y=loga(x+c)(a,c为常数,其中a>0,a≠1)的图象如图,则下列结论成立的是()A.a>1,c>1B.a>1,0
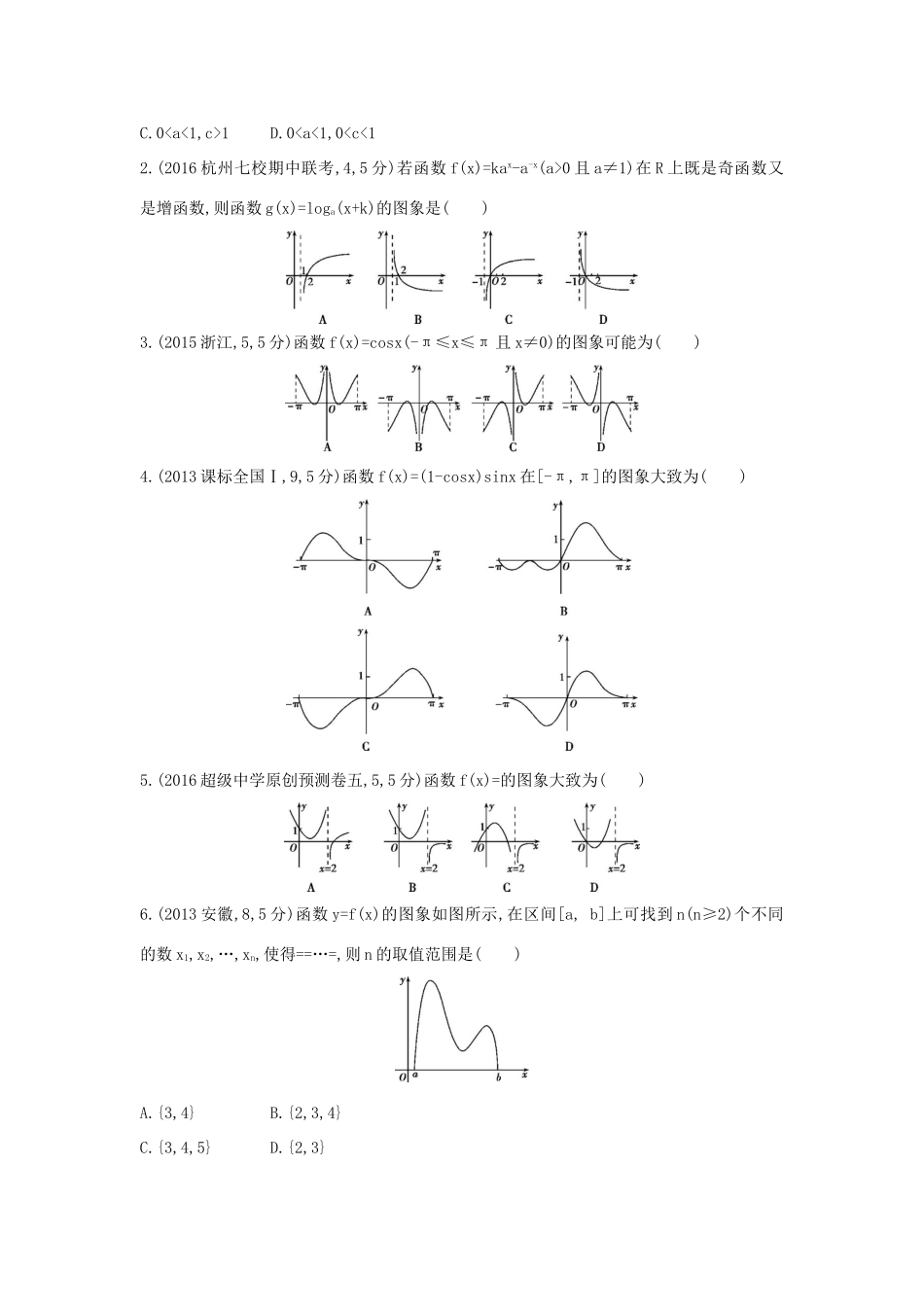
1D.00且a≠1)在R上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是()3.(2015浙江,5,5分)函数f(x)=cosx(-π≤x≤π且x≠0)的图象可能为()4.(2013课标全国Ⅰ,9,5分)函数f(x)=(1-cosx)sinx在[-π,π]的图象大致为()5.(2016超级中学原创预测卷五,5,5分)函数f(x)=的图象大致为()6.(2013安徽,8,5分)函数y=f(x)的图象如图所示,在区间[a,b]上可找到n(n≥2)个不同的数x1,x2,…,xn,使得==…=,则n的取值范围是()A.{3,4}B.{2,3,4}C.{3,4,5}D.{2,3}7.(2015浙江名校(杭州二中)交流卷六,1)函数y=lg的图象关于点M对称,则点M的坐标是()A.B.C.D.8.(2015浙江镇海中学测试卷四,10,5分)设函数f(x)的定义域为D,若存在非零实数m,满足对于任意的x∈M(M⊆D),均有x+m∈D,且f(x+m)≥f(x),则称f(x)为M上的m高调函数.如果定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2,且f(x)为R上的4高调函数,那么实数a的取值范围是()A.[-1,1]B.(-1,1)C.[-2,2]D.(-2,2)9.(2016超级中学原创预测卷四,8,5分)已知函数f(x)=1-|2x-1|,x∈[0,1],记fn(x)=f[fn-1(x)],n≥2,n∈N*,且f1(x)=f(x),则g(x)=f4(x)-的零点个数是()A.10B.12C.13D.1510.(2015杭州学军中学第十次月考)已知函数f(x)=-,则f(x)的递增区间为,函数g(x)=f(x)-的零点有个.A组基础题组1.D分01两种情况,易知A、B、C均错,选D.2.D由于函数f(x)的定义域为R,且满足f(-x)=f(x),所以函数f(x)为偶函数,其图象关于y轴对称,排除选项A,C;又f(0)=1>0,排除选项B,故选D.3.D化简得f(x)=故选D.4.B当00,则A错.故选B.5.C函数f(x)的定义域为{x|x≠-c},由题中图象可知-c=xP>0,即c<0,排除B.令f(x)=0,可得x=-,则xN=-,又xN>0,则<0.所以a,b异号,排除A,D.故选C.6.D与曲线y=ex关于y轴对称的图象对应的函数为y=e-x,将函数y=e-x的图象向左平移1个单位长度即得y=f(x)的图象,∴y=f(x)=e-(x+1)=e-x-1,故选D.7.B因为当x∈R时,函数f(x)=a|x|(a≠1)始终满足0<|f(x)|≤1,所以00时,函数y=loga=-logax,显然此时函数单调递增,故选B.8.C在同一直角坐标系中作出函数g(x)=|x+1|,h(x)=x2-2x+的图象,可得f(x)=结合图象可知函数无最大值,函数的最小值为f=.9.B作出函数y=f(x)的图象,如图所示,再作出与函数y=2x2+4x+1(x<0)的图象关于原点对称的图象,记为曲线C,发现曲线y=(x≥0)与曲线C有且仅有两个交点,∴满足条件的对称点有两对,故选B.10.答案∪解析函数f(x)=-a,x≠0有且仅有3个零点,即函数y=,x≠0与y=a的图象有且仅有3个不同的交点.又y==可知当