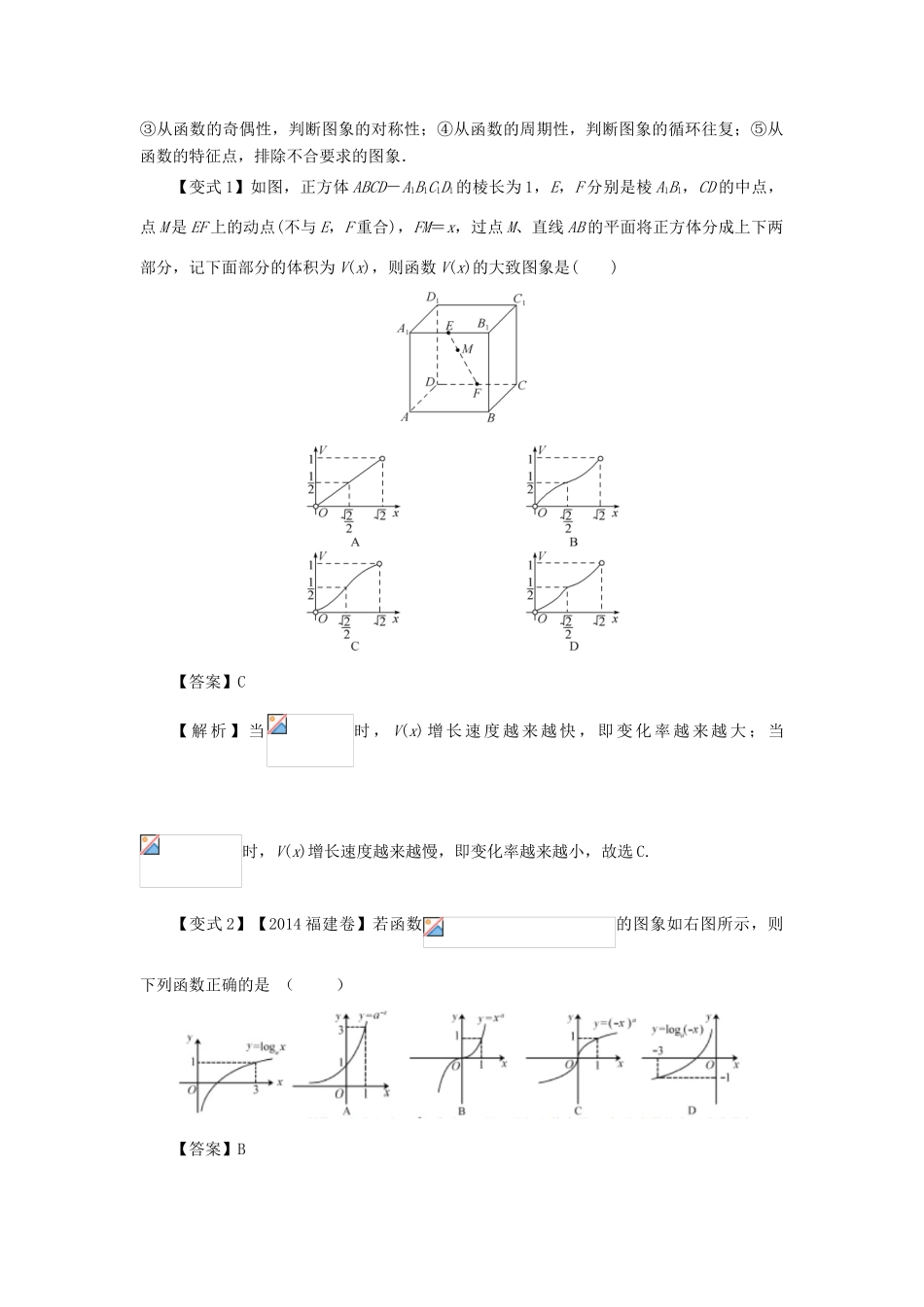
考点8函数图象【考纲要求】能用变换法作函数图象,并会运用函数图象理解和研究函数的性质.【命题规律】函数的图象与性质历来是高考的重点,也是热点,对于函数图象的考查体现在两个方面:一是识图;二是用图,即通过函数的图象,利用数形结合的思想方法解决问题.函数图象问题在选择题或填空题中会单独考查图象的判断,在解答题中也会涉及作图用图问题.【典型高考试题变式】(一)根据函数的解析式判断图象例1.【2016新课标1】函数在的图象大致为()【答案】D【名师点睛】函数中的识图题多次出现在高考试题中,也可以说是高考的热点问题,这类题目一般比较灵活,对解题能力要求较高,故也是高考中的难点,解决这类问题的方法一般是利用间接法,即由函数性质排除不符合条件的选项.【变式1】函数的图象大致是()【答案】C【解析】由题意得,x≠0,排除A;当x<0时,x3<0,3x-1<0,所以>0,排除B;又因为x→+∞时,→0,所以排除D,故选C.【变式2】若变量x,y满足|x|-ln=0,则y关于x的函数图象大致是()【答案】B【解析】由|x|-ln=0,得y==利用指数函数图象可知选B.(二)已知函数图象判断图象例2.【2012湖北卷】已知定义在区间上的函数的图象如图所示,则的图象为()【答案】B【解析】特殊值法:当时,,故可排除D项;当时,,故可排除A,C项;所以由排除法知选B.【名师点睛】函数图象的识辨可从以下方面入手:①从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置;②从函数的单调性,判断图象的变化趋势AO12xBO12xCO12xDO12x③从函数的奇偶性,判断图象的对称性;④从函数的周期性,判断图象的循环往复;⑤从函数的特征点,排除不合要求的图象.【变式1】如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF上的动点(不与E,F重合),FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面部分的体积为V(x),则函数V(x)的大致图象是()【答案】C【解析】当时,V(x)增长速度越来越快,即变化率越来越大;当时,V(x)增长速度越来越慢,即变化率越来越小,故选C.【变式2】【2014福建卷】若函数的图象如右图所示,则下列函数正确的是()【答案】B【解析】由函数的图象可知,所以,,及均为减函数,只有是增函数,故选B.(三)已知函数图象判断字母的符号例3.【2015安徽卷】函数的图象如图所示,则下列结论成立的是()A.,,B.,,C.,,D.,,【答案】C【名师点睛】函数图象的分析判断主要依据两点:一是根据函数的性质,如函数的奇偶性、单调性、值域、定义域等;二是根据特殊点的函数值,采用排除的方法得出正确的选项.本题主要是通过函数解析式判断其定义域,并在图形中判断出来,另外,根据特殊点的位置能够判断的正负关系.【变式1】(2017西安模拟)已知函数f(x)=loga2x+b-1(a>0,a≠1)的图象如图所示,则a,b满足的关系是()A.0
1.函数图象与y轴的交点坐标为(0,logab),由函数图象可知-1