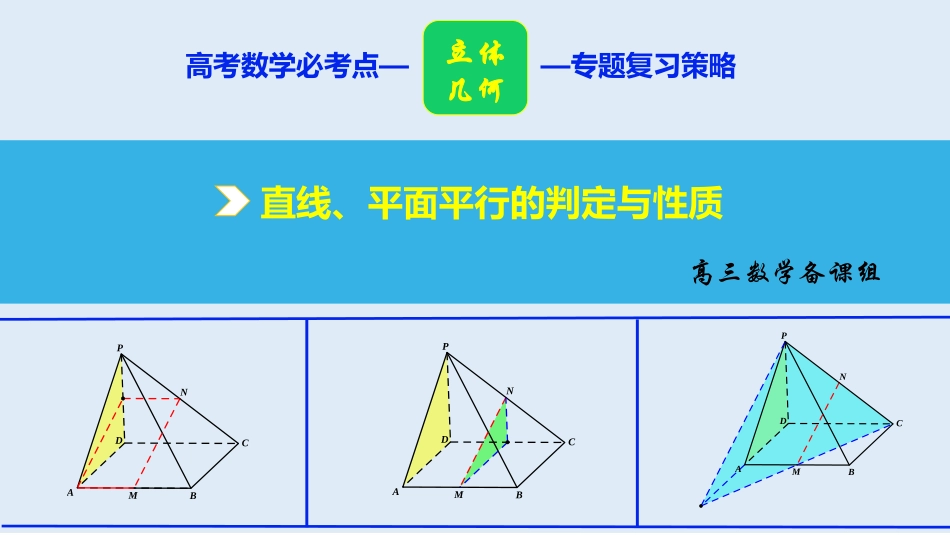
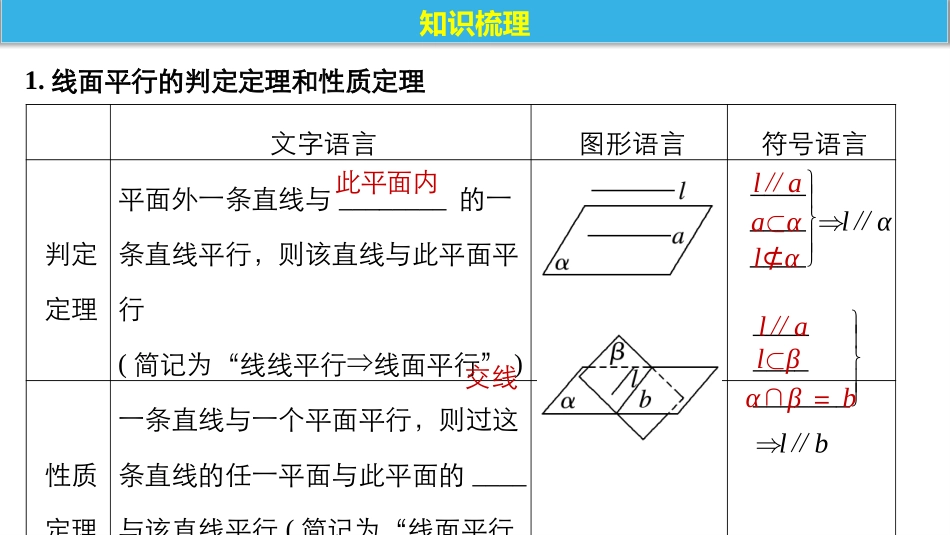
高考数学必考点——专题复习策略立体几何MNBDCAPMNBDCAPMNBDCAP直线、平面平行的判定与性质高三数学备课组2019考纲考情文字语言图形语言符号语言判定定理平面外一条直线与________的一条直线平行,则该直线与此平面平行(简记为“线线平行⇒线面平行”)性质定理一条直线与一个平面平行,则过这条直线的任一平面与此平面的____与该直线平行(简记为“线面平行⇒线线平行”)1.线面平行的判定定理和性质定理知识梳理此平面内交线____________⇒l∥α_______________⇒l∥bl∥aa⊂αl⊄αl∥al⊂βα∩β=b文字语言图形语言符号语言判定定理一个平面内的两条________与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)性质定理如果两个平行平面同时和第三个平面____,那么它们的_____平行________________________⇒α∥β2.面面平行的判定定理和性质定理相交直线a∥βb∥β相交____________________⇒a∥b交线a∩b=Pa⊂αb⊂αα∥βα∩γ=aβ∩γ=b知识梳理重要结论:(1)垂直于同一条直线的两个平面平行,即若a⊥α,a⊥β,则α∥β.(2)垂直于同一个平面的两条直线平行,即若a⊥α,b⊥α,则a∥b.(3)平行于同一个平面的两个平面平行,即若α∥β,β∥γ,则α∥γ.【知识拓展】知识梳理1.下列命题中正确的是()A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.平行于同一条直线的两个平面平行D.若直线a,b和平面α满足a∥b,a∥α,b⊄α,则b∥α√教材:《必修2》P61A组T1走进教材知者加速:《赢在微点》P138例1(1)2.若平面α∥平面β,直线a∥平面α,点B∈β,则在平面β内且过B点的所有直线中()A.不一定存在与a平行的直线B.只有两条与a平行的直线C.存在无数条与a平行的直线D.存在唯一与a平行的直线√走出误区3.设α,β,γ为三个不同的平面,a,b为直线,给出下列条件:①a⊂α,b⊂β,a∥β,b∥α;②α∥γ,β∥γ;③α⊥γ,β⊥γ;④a⊥α,b⊥β,a∥b.其中能推出α∥β的条件是______.(填上所有正确的序号)②④知者加速:《赢在微点》P138例1(2)4.如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则四边形EFGH的形状为___________.平行四边形走出误区知者加速:《赢在微点》P138例1(2)典例剖析例如图,四棱锥P-ABCD,底面ABCD为平行四边形,M、N分别为AB、PC的中点,平面PAD∩平面PBC=直线l.(Ⅰ)判断BC与直线l的位置关系,并证明你的结论;(Ⅱ)求证:MN‖平面PAD.MNBDCAPl知者加速:《赢在微点》P139例2典例剖析例如图,四棱锥P-ABCD,底面ABCD为平行四边形,M、N分别为AB、PC的中点,平面PAD∩平面PBC=直线l.(Ⅰ)判断BC与直线l的位置关系,并证明你的结论;(Ⅱ)求证:MN‖平面PAD.MNBDCAP变式训练变式如图,三棱柱ADF-BCE的侧面ABCD和ABEF均为平行四边形,M、N分别为对角线AC、FB上的三等分点,满足AC=3AM、FB=3FN.求证:MN‖平面ADFCBADFEMN变式训练变式如图,三棱柱ADF-BCE的侧面ABCD和ABEF均为平行四边形,M、N分别为对角线AC、FB上的三等分点,满足AC=3AM、FB=3FN.求证:MN‖平面ADFCBADFEMN课堂小结线线平行线面平行面面平行(1)若一条直线平行于一个平面内的一条直线,则这条直线平行于这个平面.()(2)若一条直线平行于一个平面,则这条直线平行于这个平面内的任一条直线.()(3)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.()(4)如果两个平面平行,那么分别在这两个平面内的两条直线平行或异面.()(5)若直线a与平面α内无数条直线平行,则a∥α.()(6)若α∥β,直线a∥α,则a∥β.()自我检测×××√××1.判断下列结论是否正确(请在括号中打“√”或“×”)2.(2016·全国Ⅲ)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.证明:MN∥平面PAB.自我检测当堂检测ATNTTPB、,连接中点证明:取PABMNPABATPABMNATMNATNMAMNTADAMBCAMBCNTBCNTPBPCTN平面平面平面又为平行四边形四边形又的中点、分别为、//,////232,//221,//快马加鞭,君为先,自古英雄出少年!同学们,加油!!!