341相似三角形的判定 (3)VIP免费

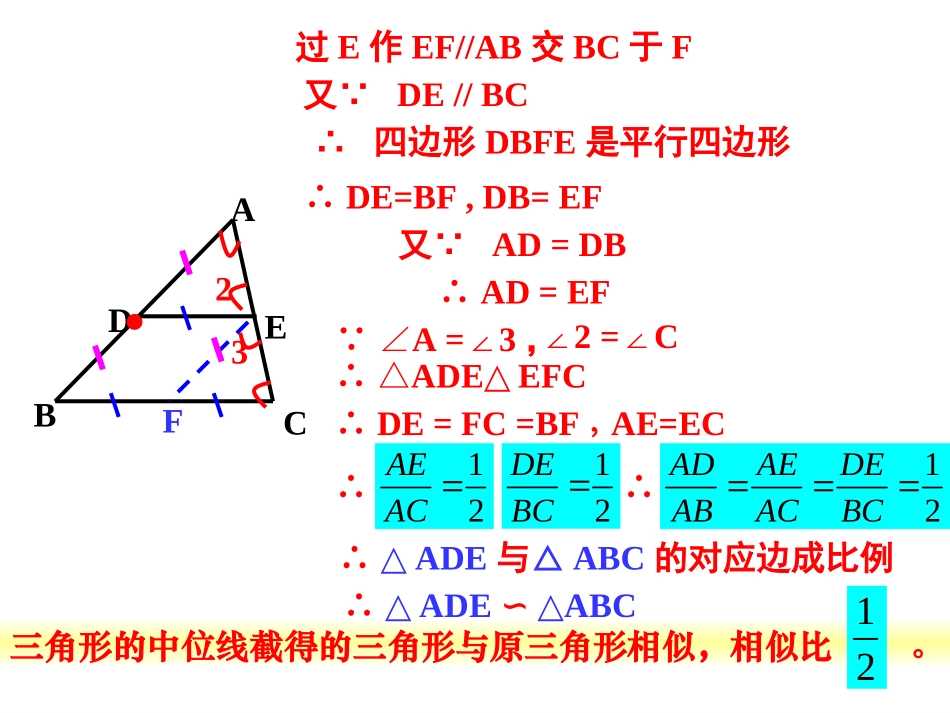
已知：DE//BC，且D是边AB的中点，DE交AC于E.猜想：△ADE与△ABC有什么关系?并证明。ABCDE证明:且∠A=A∠ DE//BC∴∠1=B∠，∠2=C∠∴△ADE与△ABC的对应角相等相似。12三角形的中位线截得的三角形与原三角形相似，相似比。∴四边形DBFE是平行四边形∴DE=BF,DB=EF∴△ADE∽ABC△ABCDEF过E作EF//AB交BC于F又 DE//BC又 AD=DB∴AD=EF ∠A=3∠，∠2=C∠∴△ADEEFC△∴DE=FC=BF，∴∴∴△ADE与△ABC的对应边成比例23AE=EC12AEAC12DEBC12ADAEDEABACBC12已知：DE//BC，△ADE与△ABC有什么关系?猜想：△ADE与△ABC有什么关系?相似。ABCDEF当点D在AB上任意一点时，上面的结论还成立吗？12你能证明吗？定义判定方法全等三角形相似三角形回顾并思考三角、三边对应相等的两个三角形全等三角对应相等,三边对应成比例的两个三角形相似角边角ASA角角边AAS边边边SSS边角边SAS斜边与直角边HL判定三角形相似，是不是也有这么多种方法呢？边边边SSS已知：△ABC∽△A1B1C1.A1B1C1ABC111111.ABBCACABBCAC求证：有效利用判定定理一去求证。探究1证明：在线段（或它的延长线）上截取，过点D作，交于点E根据前面的定理可得.11AB1ADAB11DEBC∥11AC1111ADEABC∽A1B1C1ABCDE11111111ADAEDEABBCAC1111111,ABBCACADABABBCAC1AEAC,DEBC111ABCABC∽1ADEABC≌∴又A1B1C1ABCDE∴111111111,AEDEBCACBCBCACAC∴∴（SSS）1111ADEABC∽ ∴如果两个三角形的三组对应边成比例，那么这两个三角形相似。知识要点知识要点判定三角形相似的定理之一△ABC∽△A1B1C1.111111,ABBCACABBCAC即：如果那么A1B1C1ABC三边对应成比例，两三角形相似。边边边SSS√ABBCACADDEAE，求证：∠BAD=CAE∠。ADCEB∴ΔABCΔ∽ADE∴∠BAC=∠DAE∴∠BAC－∠DAC=∠DAE－∠DAC即∠BAD=CAE∠小练习小练习已知：解： ABBCACADDEAE，边角边SAS探究2已知：△ABC∽△A1B1C1.A1B1C1ABC1111,ABBCkABBC求证：∠B=∠B1.你能证明吗？如果两个三角形的两组对应边成比例，并且相应的夹角相等，那么这两个三角形相似。知识要点知识要点判定三角形相似的定理之二两边对应成比例，且夹角相等，两三角形相似。边角边SAS√A1B1C1ABC△ABC∽△A1B1C1.即：如果1111,ABBCkABBC∠B=∠B1.那么大家一起画一个三角形，三个角分别为60°、45°、75°，大家画出的三角形相似吗?同桌的同学，通过测量对应边的长度进行比较。探究3即：如果一个三角形的三个角分别与另一个三角形的三个角对应相等，那么这两个三角形_______。相似一定需要三个角吗？角边角ASA角角边AAS角角AAA1B1C1ABC已知：△ABC∽△A1B1C1.求证：∠A=∠A1，∠B=∠B1.你能证明吗？如果两个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。知识要点知识要点判定三角形相似的定理之三两角对应相等，两三角形相似。角角AAA1B1C1ABC△ABC∽△A1B1C1.即：如果那么√∠A=∠A1，∠B=∠B1.如果两个三角形有一个内角对应相等，那么这两个三角形一定相似吗？一角对应相等的两个三角形不一定相似。△ACDCBDABC∽△∽△小练习小练习找出图中所有的相似三角形。“双垂直”三角形BDAC有三对相似三角形：△ACDCBD∽△△CBDABC∽△△ACDABC∽△例题例题已知：DEBC∥，EFAB.∥求证：△ADEEFC.∽△AEFBCD解: DE∥BC，EF∥AB（已知）∴∠ADE＝∠B＝∠EFC（两直线平行，同位角相等）∠AED＝∠C（两直线平行，同位角相等）∴△ADE∽△EFC（两个角分别对应相等的两个三角形相似）探究4已知：△ABC∽△A1B1C1.1111,ABBCkABBC求证：你能证明吗？HLABCA1B1C1Rt△ABC和Rt△A1B1C1.如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。知识要点知识要点判定三角形相似的定理之四HLABC△ABC∽△A1B1C1.即：如果那么√A1B1C11111,ABBCkABBCRtABC△和RtA△1B1C1.平行于三角形一边的直线与其他两边相交,截得的三角形与原三角形相似;两边对应成比例且夹角相等,两三角形相似.（SAS）相似三角形的判定方法三边对应成比例,两三角形相似.（SSS）两角分别相等的两个三角...