233-234直线与平面、平面与平面垂直的性质选用VIP免费

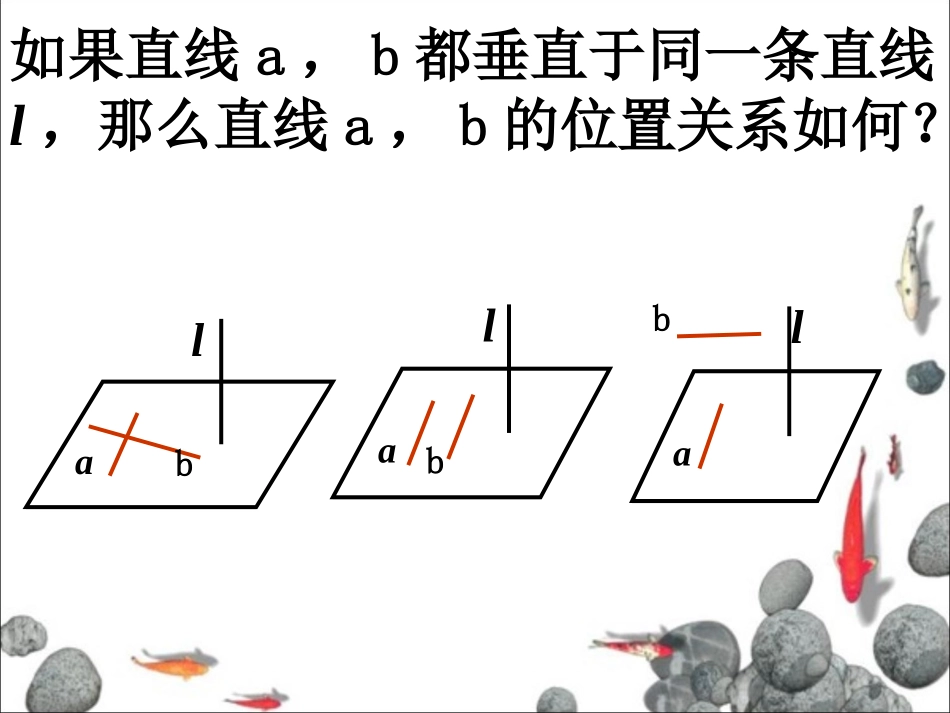
直线与平面平面与平面垂直的性质问题提出1.直线与平面垂直的定义是什么？如何判定直线与平面垂直？2.直线与平面垂直的判定定理，解决了直线与平面垂直的条件问题；反之，在直线与平面垂直的条件下，能得到哪些结论？如果直线a，b都垂直于同一条直线l，那么直线a，b的位置关系如何？ablablabl复习引入问题：若一条直线与一个平面垂直，则可得到什么结论？若两条直线与同一个平面垂直呢？(二)线面垂直性质定理的探究11、直观感知、直观感知——猜想定理猜想定理五、过程设计讲授新课BD'C'A'B'ADC(1)如图，长方体ABCD-A'B'C'D'中，棱AA'、BB'、CC'、DD'所在直线都垂直于平面ABCD，它们之间有什么位置关系？讲授新课(2)如图，已知直线a⊥、b⊥，那么直线a、b一定平行吗？我们能否证明这一事实的正确性呢？ab已知：求证：a⊥平面，b⊥平面，a∥b．ab已知：求证：a⊥平面，b⊥平面，a∥b．abO已知：求证：a⊥平面，b⊥平面，a∥b．abb'O已知：求证：a⊥平面，b⊥平面，a∥b．abb'O已知：求证：a⊥平面，b⊥平面，a∥b．abb'cO已知：求证：a⊥平面，b⊥平面，a∥b．abb'cO(反证法)已知：求证：a⊥平面，b⊥平面，a∥b．abb'cO(反证法)定理垂直于同一个平面的两条直线平行.ab线面垂直性质定理：垂直于同一个平面的两条直线平行//aabbab垂直于同一条直线的两条直线平行平面中空间中√╳B1C1D1A1ABCD设直线a,b分别在正方体ABCD-A‘B’C‘D’中两个不同的面所在平面内,欲使a//b,a,b应该满足什么条件?①a,b分别在正方体的两个相对面内,此时直线a,b必为这两个面与第三个平面交线.②a,b分别在正方体的两个相邻面内,此时直线a,b必与这两个面的交线平行.）（相垂直垂直，则这两条直线互另一条直线与这个平面）一条直线在平面内，（）（两条直线平行）垂直于同一个平面的（）（两个平面互相平行）垂直于同一条直线的（：判断下列命题是否正确练习：.3.2.1.1._____________,,,.2的位置关系是与，则且和平面已知直线bababaab√√√bb或,//小试牛刀理论迁移例1如图，已知于点A，于点B，求证：.,,lCACB,,aaAB//alABCαβla（2）若，求证：MN面PCD例2如图，已知矩形ABCD所在平面，M、N分别是AB、PC的中点求证：（1）PA;MNCD45PDAPABCDMNEA1D1B1C1CBAD面面垂直的性质αβ如果α⊥β(1)α里的直线都和β垂直吗？DEF(2)什么情况下α里的直线和β垂直？面面垂直的性质•面面垂直性质定理：两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。面面垂直线面垂直αβaAllaala定理剖析1)面面垂直线面垂直；（线是一个平面内垂直于两平面交线的一条直线）αβCDAB2）它为判定和作出线面垂直提供依据。①线在平面内；关键点：②线垂直于交线。例如图，已知平面，β，⊥β，直线a满足a⊥β，a，试判断直线a与平面的位置关系.baβ练习1.教材P.73练习第1、2题练习2.下列命题中，正确的是()A.过平面外一点，可作无数条直线和这个平面垂直B.过一点有且仅有一个平面和一条定直线垂直C.若a、b异面，过a一定可作一个平面与b垂直D.若a、b异面，过不在a、b上的点，一定可以作一个平面和a、b都垂直.求证：若两个相交平面都垂直于另一个平面，则这两个平面的交线垂直于这个平面.γαβa已知：αγ⊥，βγ,α∩β=а,⊥求证：aγ.⊥拓展提高例垂直于同一平面的两平面的交线垂直于这个平面。已知：αγ⊥，βγ,α∩β=а,⊥求证：aγ.⊥证法一：γαβabcPMN设α∩γ=b,β∩γ=c,在γ内任取一点P，作PMb⊥于M，PNC⊥于N.因为αγ⊥，βγ⊥，所以PMα⊥，PNβ.⊥因为α∩β=a，所以PMa⊥，PN⊥a，所以aγ.⊥线线垂直线面垂直γαβa已知：αγ⊥，βγ,α∩β=а,⊥求证：aγ.⊥证法二：Pb任取Pa∈，过点P作b⊥γ.∩∩因为α⊥γ，所以bα，因为β⊥γ，因此bβ，故α∩β=b.由已知α∩β=a，所以a与b重合，所以a⊥γ.同一法γαβa已知：αγ⊥，βγ,α∩β=⊥а,求证：aγ.⊥证法三：bcb′c′设αγ⊥于b，βγ⊥于c...