2.3.2双曲线的简单几何性质课件VIP免费

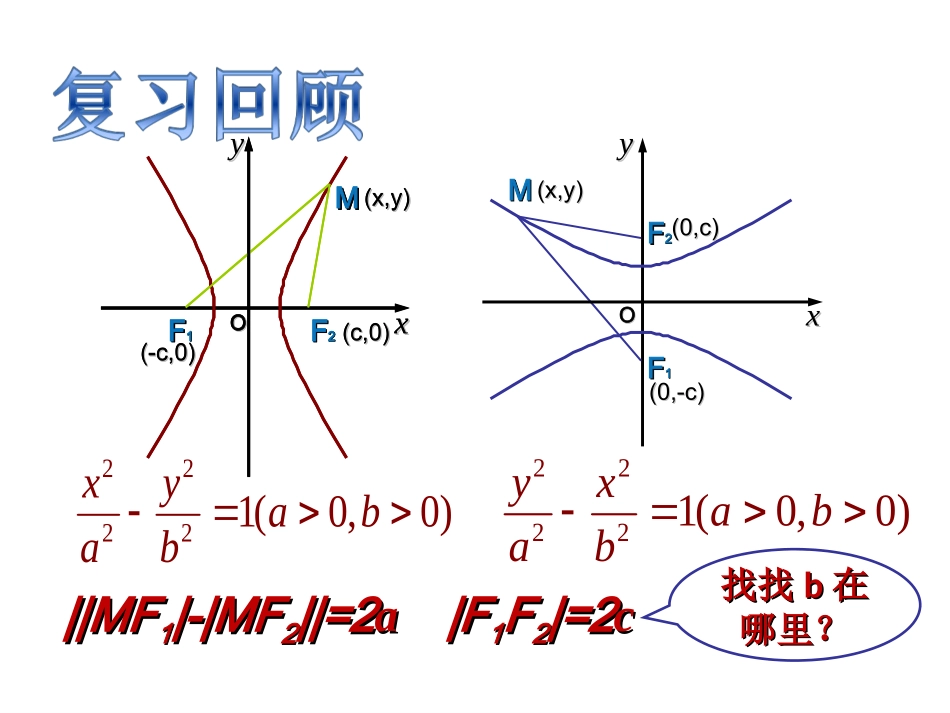
FF22FF11MMxxOOyy(-c,0)(-c,0)(x,y)(x,y)(c,0)(c,0)||MF||MF11|-|MF|-|MF22||=2||=2aa|F|F11FF22|=2|=2cc找找找找bb在在哪里？哪里？FF22FF11MMxxOO(-c,0)(-c,0)(x,y)(x,y)(c,0)(c,0)xxyyFF11(0,-c)(0,-c)MM(x,y)(x,y)FF22(0,c)(0,c)OO22221(0,0)yxabab22221(0,0)xyabab图中双曲线的标准方程为图中双曲线的标准方程为请写出图中各点的坐标．请写出图中各点的坐标．221169xy双曲线与双曲线与yy轴没有交点，我们仍把轴没有交点，我们仍把BB11，，BB22点画到点画到yy轴轴上，并取坐标（如图）．构造与椭圆相似的特征三角形上，并取坐标（如图）．构造与椭圆相似的特征三角形(-4,0)(-4,0)(4,0)(4,0)(-5,0)(-5,0)(5,0)(5,0)(-3,0)(-3,0)(3,0)(3,0)aabbccaa=4=4，，bb=3=3，，所以所以cc=5=5△△BB22FF22OO叫双曲线的叫双曲线的特征三角形特征三角形..纵坐标的范围：纵坐标的范围：RR横坐标的范围：横坐标的范围：xx-a-a或或xxaa(-(-aa,0),0)((aa,0),0)((00,b),b)(0,-b)(0,-b)特征三角形特征三角形△△BB22AA22OO三边长分别为三边长分别为||BB22AA22|=|=cc，，||OOAA22|=|=aa，，||OBOB22|=|=bb．．aabbcc顶点（1）双曲线与对称轴的交点，叫做双曲线的顶点xyo-b1B2Bb1A2A-aa)0,()0,(21aAaA、顶点是实轴与虚轴等长的双曲线叫等轴双曲线（2）)0(22mmyx线段线段AA11AA22叫椭圆的实轴，长为叫椭圆的实轴，长为22aa，，AA11，，AA22为实轴顶点为实轴顶点；；线段线段BB11BB22叫椭圆的虚轴，长为叫椭圆的虚轴，长为22bb，，BB11，，BB22为虚轴顶点为虚轴顶点．．xyo-aa(-x,-y)(-x,y)(x,y)(x,-y)双曲线关于双曲线关于yy轴对称轴对称双曲线关于双曲线关于xx轴对轴对称称双曲线关于原点对称双曲线关于原点对称M(x,y)1A2A1B2BN(x,y’)Q:的位置关系它与xaby:的位置的变化趋势它与xaby的下方在xaby慢慢靠近xyoxabyxabyab)0(22xaxaby分的方程为双曲线在第一象限内部xabybabyax的渐近线为双曲线)0,0(12222（1）的渐近线为等轴双曲线)0(22mmyx（2）xy利用渐近线可以较准确的画出双曲线的草图（3）与椭圆相类似与椭圆相类似,,双曲线的焦距与实轴双曲线的焦距与实轴长的比称为双曲线的离心率，用长的比称为双曲线的离心率，用ee表示，即表示，即,1ceeaaabbcc（1）定义：双曲线的叫做的比双曲线的焦距与实轴长,ace离心率。c>a>0e>1e是表示双曲线开口大小的一个量,e越大开口越大（2）e的范围：（3）e的含义：11)(2222eacaacab也增大增大且时，当abeabe,),,0(),1(的夹角增大增大时，渐近线与实轴eace222bac二四个参数中，知二可求、、、在ecba（4）等轴双曲线的离心率e=?2(5)的双曲线是等轴双曲线离心率2eA1A2B1B2abc222abcx0y几何意义焦点在y轴上的双曲线的几何性质口答双曲线标准方程：YX12222bxay0aybx双曲线性质：1、范围：y≥a或y≤-a2、对称性：关于x轴，y轴，原点对称。3、顶点B1（0，-a），B2（0，a）4、轴：实轴B1B2;虚轴A1A2A1A2B1B25、渐近线方程：6、离心率：e=c/aF2F2o如何记忆双曲线的渐进线方程？练习1、标准方程32822yx81922yx422yx1254922yx2a2b范围顶点焦点离心率渐进线|x|≥0,240,6423exy424618|x|≥3(±3,0)0,10310ey=±3x44|y|≥2(0,±2)2e22,0xy1014|y|≥5(0,±5)74,0574exy752824求双曲线求双曲线99yy22-16-16xx22=144=144的实半轴的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程．长和虚半轴长、焦点坐标、离心率、渐近线方程．解：把方程化为标准方程解：把方程化为标准方程::所以所以::aa=4=4，，bb=3=3，，即即221169yx1695c渐近线方程为．渐近线方程为．实半轴长实半轴长aa=4=4，虚半轴长，虚半轴长bb=3=3；；离心率为离心率为1.251.25；；焦点坐标为焦点坐标为(0,-5),(0,5)(0,-5),(0,5)43yx求下列双曲线的焦点坐标：求下列双曲线的焦点坐标：22(1)832xy；22(2)4xy．(2)(2)先化为标准方程先化为标准方程a=2a=2，，b=2b=2，，c=c=...