定积分在几何中应用VIP免费

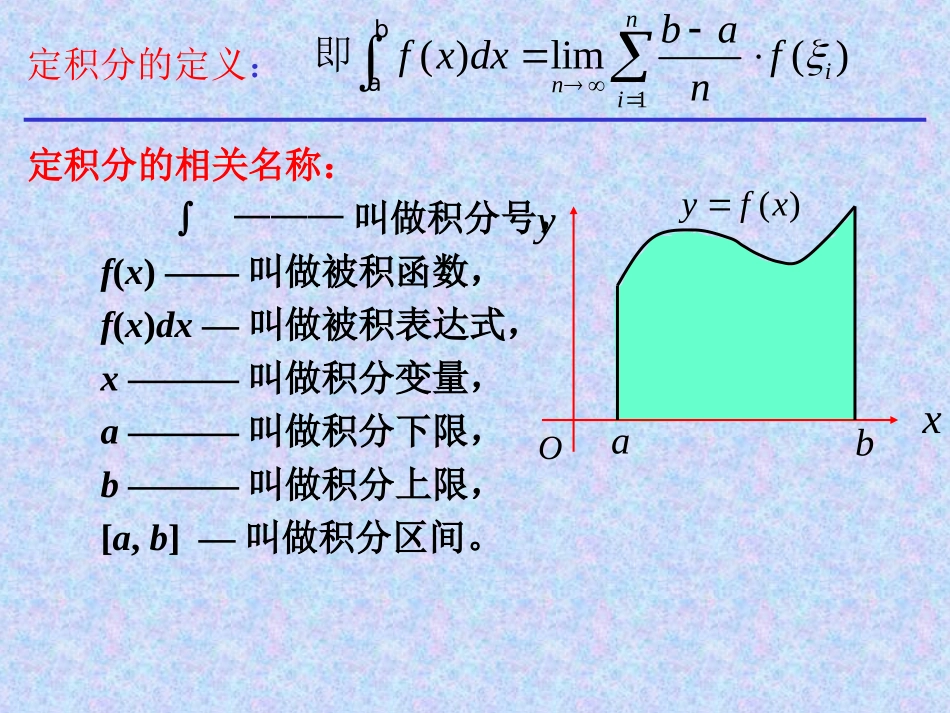
1.7.1定积分在几何中的应用一、定积分的定义11()()nniiiibafxfn小矩形面积和S=如果当n∞时，S的无限接近某个常数，这个常数为函数f(x)在区间[a,b]上的定积分，记作baf(x)dx，即f(x)dxf(i)xi。从求曲边梯形面积S的过程中可以看出,通过“四步曲”:分割---近似代替----求和------取极限得到解决.1()lim()ninibafxdxfnba即定积分的定义：定积分的相关名称：———叫做积分号，f(x)——叫做被积函数，f(x)dx—叫做被积表达式，x———叫做积分变量，a———叫做积分下限，b———叫做积分上限，[a,b]—叫做积分区间。1()lim()ninibafxdxfnba即Oabxy)(xfybaIdxxf)(iinixf)(lim10被积函数被积表达式积分变量积分下限积分上限baf(x)dxbaf(t)dtbaf(u)du。说明：(1)定积分是一个数值,它只与被积函数及积分区间有关，而与积分变量的记法无关，即（2）定义中区间的分法和i的取法是任意的.baf(x)dxbaf(x)dx-(3)(2)定积分的几何意义：Oxyabyf(x)baf(x)dxf(x)dxf(x)dx。xa、xb与x轴所围成的曲边梯形的面积。当f(x)0时，积分dxxfba)(在几何上表示由y=f(x)、特别地，当ab时，有baf(x)dx0。当f(x)0时，由yf(x)、xa、xb与x轴所围成的曲边梯形位于x轴的下方，xyOdxxfSba)]([，dxxfba)(．abyf(x)yf(x)dxxfSba)]([baf(x)dxf(x)dxf(x)dx。S上述曲边梯形面积的负值。定积分的几何意义：积分baf(x)dx在几何上表示baf(x)dxf(x)dxf(x)dx。Sabyf(x)Oxy()ygx探究:根据定积分的几何意义,如何用定积分表示图中阴影部分的面积?abyf(x)Oxy1()baSfxdx()ygx12()()bbaaSSSfxdxgxdx2()baSgxdx三:定积分的基本性质性质1.dx)]x(g)x(f[bababadx)x(gdx)x(f性质2.badx)x(kfbadx)x(fk三:定积分的基本性质定积分关于积分区间具有可加性bccabadx)x(fdx)x(fdx)x(f性质3.2121ccbccabadx)x(fdx)x(fdx)x(fdx)x(fOxyabyf(x)Ｃ性质3不论a，b，c的相对位置如何都有aby=f(x)baf(x)dxf(x)dxf(x)dx。f(x)dxcaf(x)dxf(x)dx。f(x)dxf(x)dxbcf(x)dx。cOxybaf(x)dxcaf(x)dxbcf(x)dx。例1：利用定积分的定义,计算的值.130xdx回顾一:定积分的基本性质性质1.dx)]x(g)x(f[bababadx)x(gdx)x(f性质2.badx)x(kfbadx)x(fkbccabadx)x(fdx)x(fdx)x(f性质3.回顾一:定积分的基本性质性质1.dx)]x(g)x(f[bababadx)x(gdx)x(f性质2.badx)x(kfbadx)x(fkbccabadx)x(fdx)x(fdx)x(f性质3.基本初等函数的导数公式1.2.()3.4.5.ln6.7.8.nRa'n'n-1''x'xx'x'a'若f(x)=c，则f(x)=0若f(x)=x，则f(x)=nx若f(x)=sinx，则f(x)=cosx若f(x)=cosx，则f(x)=-sinx若f(x)=a，则f(x)=a若f(x)=e，则f(x)=e1若f(x)=logx，则f(x)=xlna1若f(x)=lnx，则f(x)=x|bacx11|1nbaxn++cos|bax-sin|bax定积分公式'6)()xxbxaedeex®==ò'7)()lnbxxxaadxaaa=®=ò'15)(ln)1baxxdxx=®=ò'1)()bacxccdx=®=ò'12)nnbnaxxxnxd-®==ò'3)(sin)coscosbaxxxdx®==ò'4)(cos)sinsinbaxdxxx=-=®òln|||bax|xbae|lnxbaaa例1．计算0sinxdx解（1） '(s)sincoxx00sin(s)|cos(cos0)112xdxcox思考:()a的几何意义是什么0sinxdx?01()()|()()bbaafxdxFxFbFa22()()bc00sinxdx=_______sinxdx=_______:0,还可能是也可能取负值定积分的值可能取正值可以发现;,),36.1(x1且等于曲边梯形的面积定积分的值取正值图轴上方时当对应的曲边梯形位于.,),46.1(x2反数的相且等于曲边梯形的面积定积分的值取负值图轴下方时当对应的曲边梯形位于oxyππ211xsiny36.1图oxy11ππ2xsiny46.1图.xx),56.1(0,xx3轴下方的曲边梯形面积边梯形的面积减去位于轴上方的曲且等于位于图定积分的值为时积形面梯曲边下方的轴梯形的面积等于位于轴上方的曲边当位于.,,,,...