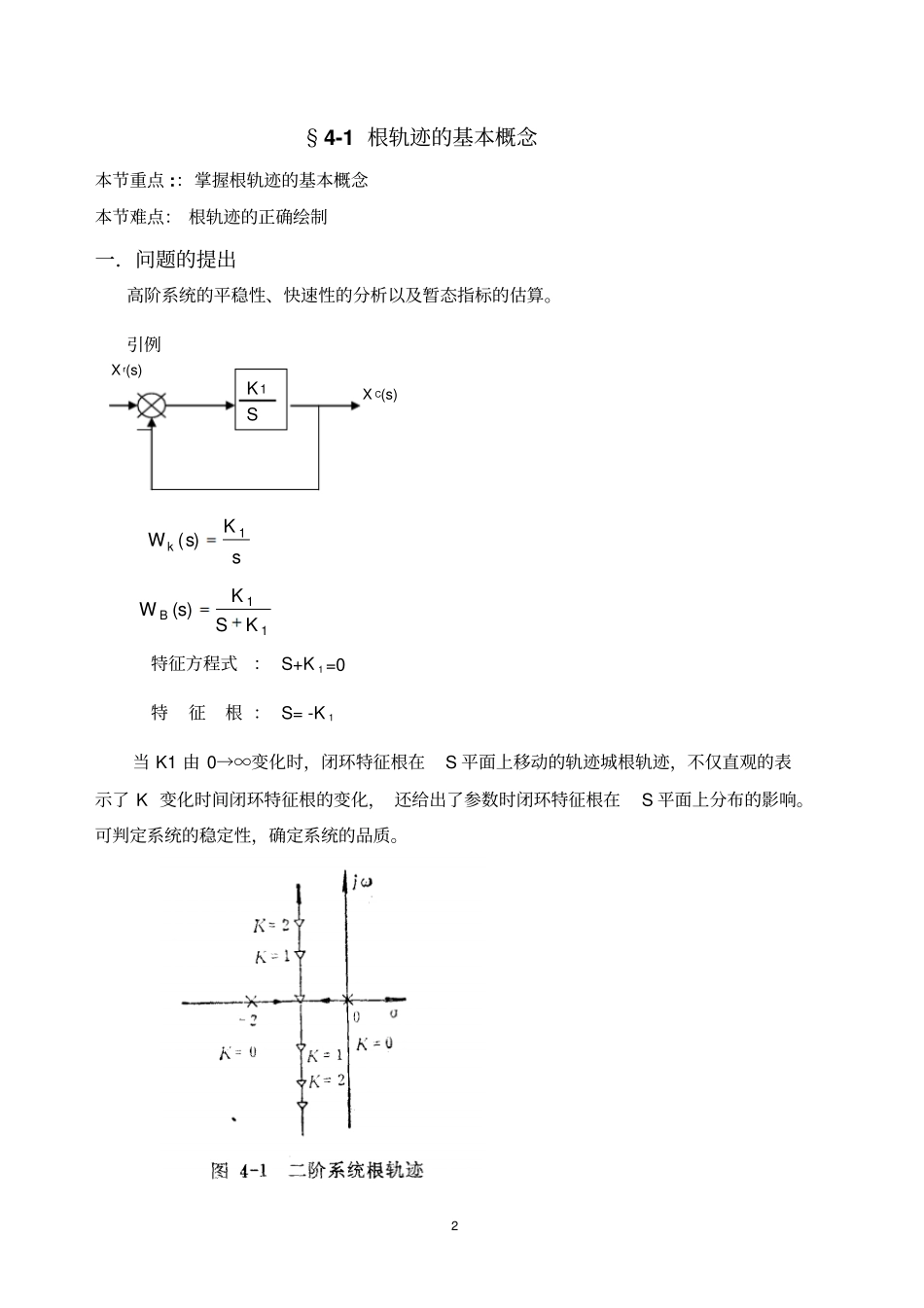
1根轨迹法一、本章内容提要:1.介绍了系统开环传递函数的极点、零点已知的条件下确定闭环系统的根轨迹法,并分析系统参量变化时对闭环极点位置的影响;2.根据闭环特征方程得到相角条件和幅值条件由此推出绘制根轨迹的基本法则;3.根轨迹绘制:常规根轨迹、参数根轨迹、零度根轨迹、时滞系统根轨迹;4.根轨迹法分析系统性能二、本章教学目的及要求:1.掌握根轨迹的基本概念;正确理解开环零极点、闭环零极点及根轨迹的含义;2.掌握控制系统根轨迹的绘制方法;3.正确绘制出不同参量变化对系统根轨迹图4.能够运用根轨迹法对控制系统进行分析;5.明确闭环零、极点的分布和系统阶跃响应的定性关系。三、本章重点、难点1.重点:根轨迹的绘制利用根轨迹分析控制系统2.关键点:根轨迹方程,幅值条件,相角条件3.难点:时滞系统根轨迹的绘制四、本章学习方法通过具体习题练习掌握根轨迹绘制方法,不要死记硬背各种绘制法则,要多总结归纳典型极、零点分布对根轨迹的大致图形。2§4-1根轨迹的基本概念本节重点::掌握根轨迹的基本概念本节难点:根轨迹的正确绘制一.问题的提出高阶系统的平稳性、快速性的分析以及暂态指标的估算。引例Xr(s)XC(s)sK)s(W1k11BKSK)s(W特征方程式:S+K1=0特征根:S=-K1当K1由0→∞变化时,闭环特征根在S平面上移动的轨迹城根轨迹,不仅直观的表示了K变化时间闭环特征根的变化,还给出了参数时闭环特征根在S平面上分布的影响。可判定系统的稳定性,确定系统的品质。K1S3J(ω)—∞σ0二、定义指当系统开环放大倍数K(通常由Kg或K1表示)由零变到无穷时,闭环极点(系统特征根)在S平面上变动的轨迹。根轨迹是根据系统开环传递函数的零、极点,求出闭环极点一般方法,是控制系统分析一种图解方法。三.根轨迹法的依据(根轨迹方程)1.已知系统系统开环传函:sDsNK)jp(S)iz(SgK)S(Wgn1jm1iK闭环系统特征方程式:1+Wk(S)=0或W(S)=-1,即1pszsKn1jjm1iig2.依据条件幅值条件:1sWk4相角条件:∠Wk(S)=±180°(1+2μ),μ=0,1,2⋯⋯或开环有限零点到S的矢量长度方程1=开环极点到S的矢量长度方程kgmnmn∑∠(s+zi)-∑∠(s+pj)=∑αi-∑βj=180)21(i=1j=1i=1j=1i—开环有限零点到S的矢量幅角βj—开环极点到S的矢量幅角3.基本思想根据幅值条件确定根轨迹上某一点对应的增益,由相角条件确定根轨迹上的某点位置。小结:根轨迹的依据§4-2根轨迹的绘制法则本节重点::掌握根轨迹的绘制方法本节难点:根轨迹的出射角和入射角,以及根轨迹和虚轴的交点一绘制常规根轨迹一般法则1.起点(Kg=0)当Kg=0闭环系统特征根即由开环系统特征方程式决定n1iig0psKsN即闭环极点也就是开环极点,根轨迹从开环极点出发。2.终点(Kg=∞)闭环系统特征方程式11)s(D)s(NgK0zssNm1ji开环零点(有限,无限)为根轨迹终点。设N(S)为m阶,有m个有限开环零点,还有n-m个无限零点1)jP(S)iZ(SKn1jm1ig53、根轨迹数与对称性条数:开环极点数,n条对称性:对称于实轴,特征根为实数或为共轭复数,根轨迹必然对称于实轴4、实轴上的根轨迹在S平面实轴上的线段上存在根轨迹的条件是:线段右侧开环零点(有限零点)和开环极点数之和为奇数。5、分离点和会合点满足:0dSdKg或0sDsNsNsD由此求出的s要代入Kg中,只有Kg为正时,才是分离式会合点。对于阶次较高,可采用图解法确定重根,在复平面若有分离点式会合点,必对称于实轴。6、渐近线(1)渐近线条数:n-m条,趋向无穷远处分之的渐近线渐近线倾角mn)21(180.......2.1.0((2)渐近线交点:伸向无穷远出与实轴交于一点坐标(-δ,j0)mnZPn1jm1iij7、根轨迹出射角和入射角出射角:)(180m1ii1n1jjsc或180sci:开环有限零点到被测起点的矢量幅角。j:除被测起点外,所有开环极点的矢量幅角入射角:)j(180n1j1m1iisr8.根轨迹与虚轴交点可用S=jω代入特征方程求解,或者利用劳斯判据确定。6根轨迹与虚轴的交点出现虚根,系统处于稳定的临界状态。故可由此确定根轨迹与虚轴的交点9、根轨迹的特性连续性:闭环系统特征方程的根是连续变化的,即根轨迹是连续变化的曲线或直线。10、闭环极点特性(1)当n>m≥2时,闭环系统极点之和等于开环系统极点之和且为数1nn...