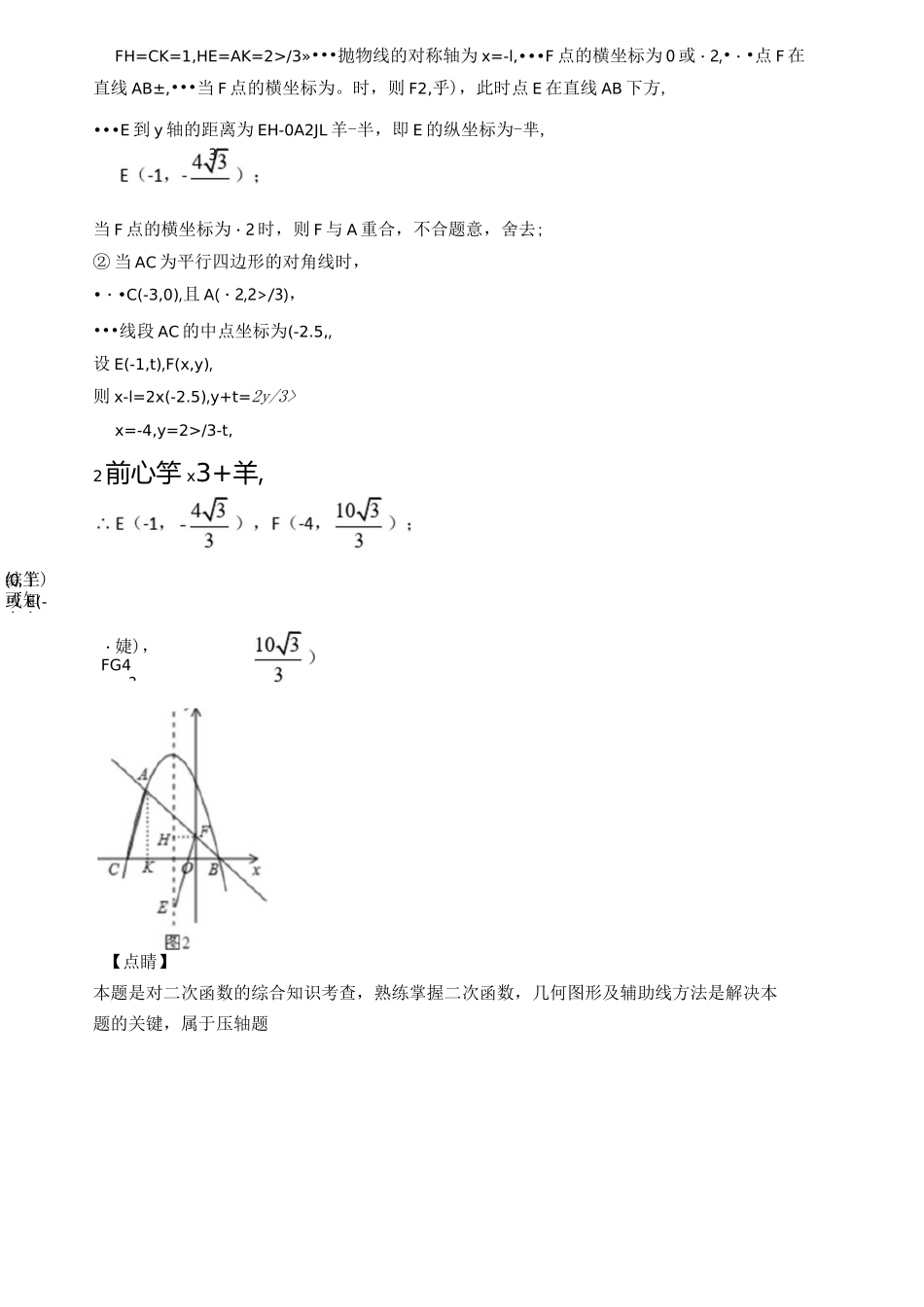
55半、5一、二次函数真题与模拟题分类汇编(难题易错题)1.在平面直角坐标系中,我们定义直线y=ax-a为抛物线y=ax23+bx+c(a、b、c为常数,aHO)的"衍生直线";有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“衍生三角形已知抛物线),=-半扌―芈X+2JJ与其"衍生直线"交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C・(1)填空:该抛物线的“衍生直线〃的解析式为,点A的坐标为,点B的坐标为:(2)如图,点M为线段CB±一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的"衍生三角形",求点N的坐标;(3)当点E在抛物线的对称轴上运动时,在该抛物线的“衍生直线"上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.【答案】(1)V--—X+—:(-2,2®;(1,0);「33【解析】【分析】(1)由抛物线的"衍生直线"知道二次函数解析式的a即可;(2)过A作AD丄y轴于点D,则可知AN=AC,结合A点坐标,则可求出ON的长,可求出N点的坐标;(3)分别讨论当AC为平行四边形的边时,当AC为平行四边形的对角线时,求出满足条件的E、F坐标即可【详解】2N点的坐标为(0,2JJ-3),(0,2^3+3):33225255产(x-R-玄a,故ARCE的面积的最大值为一言二而AACE的面积的最大值为可所以2552)‘,=_仝/!亍—也讥+2前,a=_巫,则抛物线的"衍生直线"的解析式为333竽)或2,联立两解析式求交点<尸-匹x十迹;/.A(-2,2®,B(1,0):(2)如图1,过A作AD丄y轴于点D,在),=—半亍一斗3/+2笛中,令尸0可求得/.C(-3,0),且A(-2,2>/3),•••AC=J(_2+3)U(2®=皿由翻折的性质可知AN=AC=713,•••△AMN为该抛物线的“衍生三角形",•••N在y轴上,且AD=2,在RtAAND中,由勾股定理可得DN=7AN2-AD2=A/TT4=3,OD=2>/3»•••ON=2V3-3或ON=2笛十3,•••N点的坐标为(0,2j亍-3),(0,2jT十3);图1(3)①当AC为平行四边形的边时,如图2,过F作对称轴的垂线FH,过A作AK丄x轴于点K,则有ACIIEF且AC=EF,/.ZACK=ZEFH,在厶ACK和厶EFH中ZACK=ZEFH/3»•••抛物线的对称轴为x=-l,•••F点的横坐标为0或・2,•・•点F在直线AB±,•••当F点的横坐标为。时,则F2,乎),此时点E在直线AB下方,•••E到y轴的距离为EH-0A2JL羊-半,即E的纵坐标为-芈,当F点的横坐标为・2时,则F与A重合,不合题意,舍去;②当AC为平行四边形的对角线时,••・C(-3,0),且A(・2,2>/3),•••线段AC的中点坐标为(-2.5,,设E(-1,t),F(x,y),则x-l=2x(-2.5),y+t=2y/3>x=-4,y=2>/3-t,2前心竽x3+羊,【点睛】本题是对二次函数的综合知识考查,熟练掌握二次函数,几何图形及辅助线方法是解决本题的关键,属于压轴题3・婕),FG43y=3我f+c的对称轴是辽.142如图:在平面直角坐标系中'直孙尸厂亍办轴交于点久经过点A的抛物线(1)求抛物线的解析式;(2)平移直线I经过原点0,得到直线m,点P是直线m上任意一点,PB丄x轴于点B,PC丄y轴于点C,若点E在线段0B上,点F在线段0C的延长线上,连接PE,PF,且PE=3PF.求证:PE丄PF;(3)若(2)中的点P坐标为(6,2),点E是x轴上的点,点F是y轴上的点,当PE丄PF时,抛物线上是否存在点Q,使四边形PEQF是矩形?如果存在,请求出点Q的坐标,如果不存在,请说明理由.【答案】(1)抛物线的解析式为y=x2-3x-4:(2)证明见解析;(3)点Q的坐标为(-2,6)或(2,-6)・【解析】【分析】3(1)先求得点A的坐标,然后依据抛物线过点A,对称轴是x二一列出关于a、c的方程组2求解即可;(2)设P(3a,a),则PC=3a,PB=a,然后再证明ZFPC=ZEPB,最后通过等量代换进行证明即可;(3)设E(a,0),然后用含a的式子表示BE的长,从而可得到CF的长,于是可得到点F的坐标,然后依据中点坐标公式可得到冬迟=匕■半,鱼2/+耳,从而2222可求得点Q的坐标(用含a的式子表示),最后,将点Q的坐标代入抛物线的解析式求得a的值即可.【详解】143(1)当y=o时,-X-—=0,解得X=4,即A(4,0),抛物线过点A,对称轴是x=—,33216n-12+c=0得<'.~2a~2(Cl=1解得{「抛物线的解析式为y=x2-3x-4;[c=-4(2)•・•平移直线I经过原点O,得到直线m,...