双曲线的简单几何性质双曲线的焦半径VIP免费

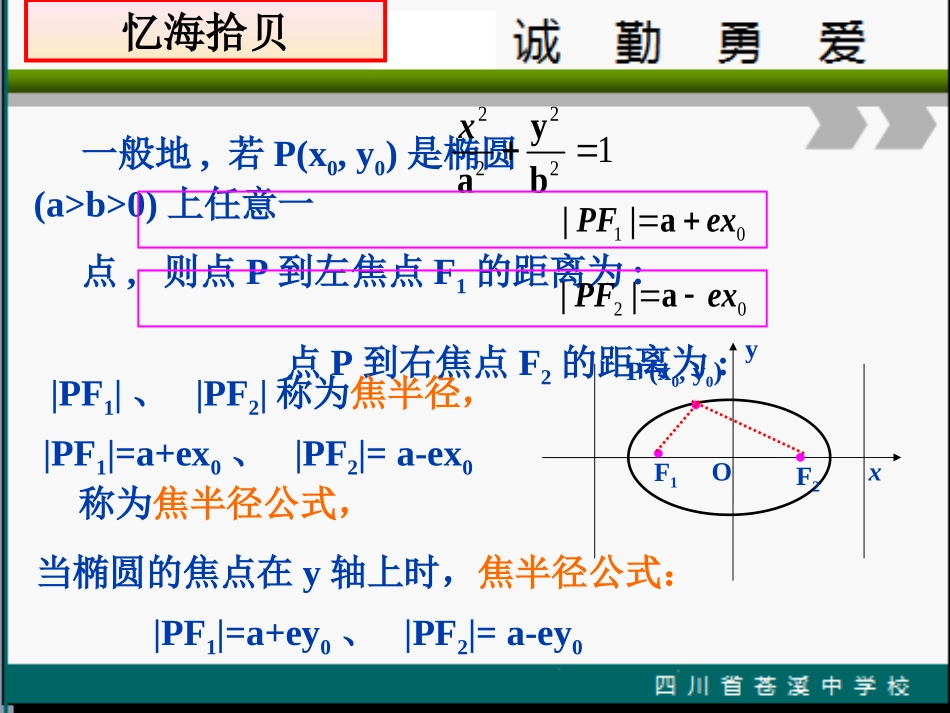
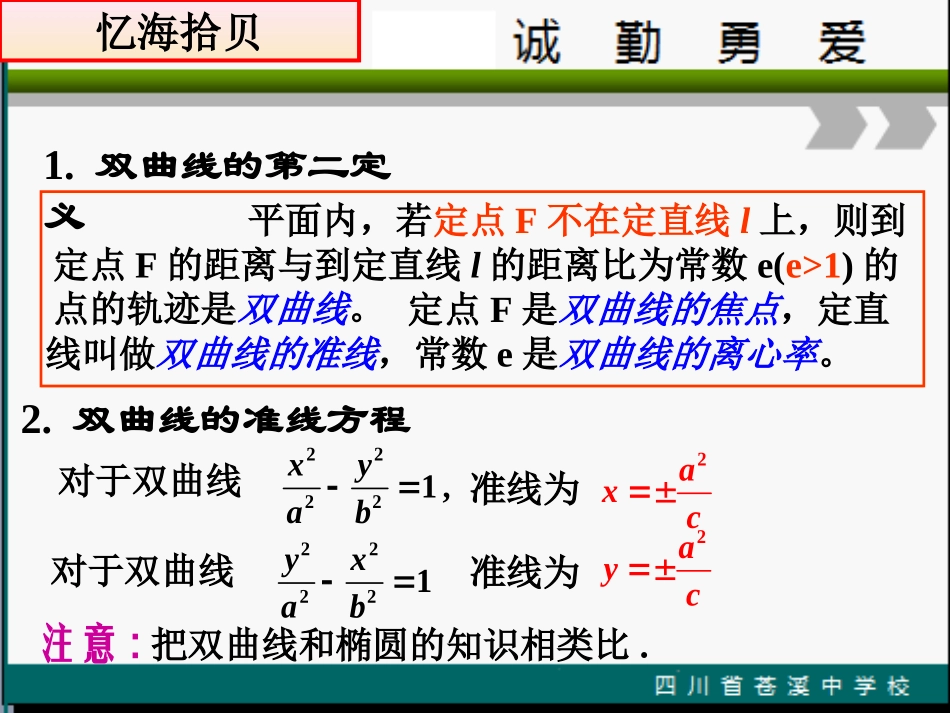
双曲线的简单几何性质双曲线的焦半径一般地,若P(x0,y0)是椭圆(a>b>0)上任意一点,则点P到左焦点F1的距离为:点P到右焦点F2的距离为:12222byaxxyOF1P(x0,y0)F201exPFa||02exPFa|||PF1|、|PF2|称为焦半径，|PF1|=a+ex0、|PF2|=a-ex0称为焦半径公式，当椭圆的焦点在y轴上时，焦半径公式：|PF1|=a+ey0、|PF2|=a-ey0忆海拾贝忆海拾贝1.双曲线的第二定义平面内，若定点F不在定直线l上，则到定点F的距离与到定直线l的距离比为常数e(e>1)的点的轨迹是双曲线。定点F是双曲线的焦点，定直线叫做双曲线的准线，常数e是双曲线的离心率。2.双曲线的准线方程对于双曲线22221,xyab准线为2axc对于双曲线22221yxab准线为2ayc注意:把双曲线和椭圆的知识相类比.例1.设M（x1,y1)是双曲线上一点,求M到双曲线两焦点F1，F2的距离.2222y1xabxyOlF2设M（x1,y1)到双曲线两焦点F1，F2相应的准线的距离为d1,d2.析：由椭圆的第二定义可知：.11MFdeF111MFed211aMFexc21caexac1exa绝对值符号能去掉吗？请你推导2MF221aMFexc21caexac1exa如果点M在双曲线右支上，绝对值符号怎样去掉？如果点M在双曲线左支上，绝对值符号怎样去掉？双曲线焦半径公式及其记忆方法：1MF1exa2MF1exaF1F2绝对值内看焦点，左加右减去绝对值看分支，左负右正1121111121MFexxaxaMFexaMF(exa)aMF(exa)点M在右支上点M在左支上xy新知探究例2.已知双曲线的一支上不同的三A（x1,y1),B(,6),C（x2,y2)与焦点F（0，5）的距离成等差数列，求y1+y2=12.22y11213x22y11213x26解：∵双曲线为∴a2=12,b2=13∴c2=2555,23,23cae152323FAy562323FB252323FCy,,FAFBFC成等差列2FAFCFB12yy12[基础练习]1.设F1，F2为双曲线的两焦点,点P在双曲线上且满足∠F1PF2=900，则⊿F1PF2的面积为.2214xy2.已知双曲线上一点P与两焦点连线垂直。则点P坐标是221xy162,22例3.设AB为过双曲线的右焦点的弦，且，求A,B两点的横坐标.221169xyAF2BF析：法1：绝对值内看焦，左加右减去绝对值看支，左负右正法2：焦半径公式12AFexaBFexa故双曲线的第二定义AB5991x,x1020练.求证：等轴双曲线上任一点P到中心的距离等于P到两个焦点距离的比例中项.析：1.设方程，画图，建系。2.写焦点坐标，a,c,e3.用焦半径公式写出︱PF1︱，︱PF2︱4.验证︱PF1︱︱PF2︱=︱PO︱2