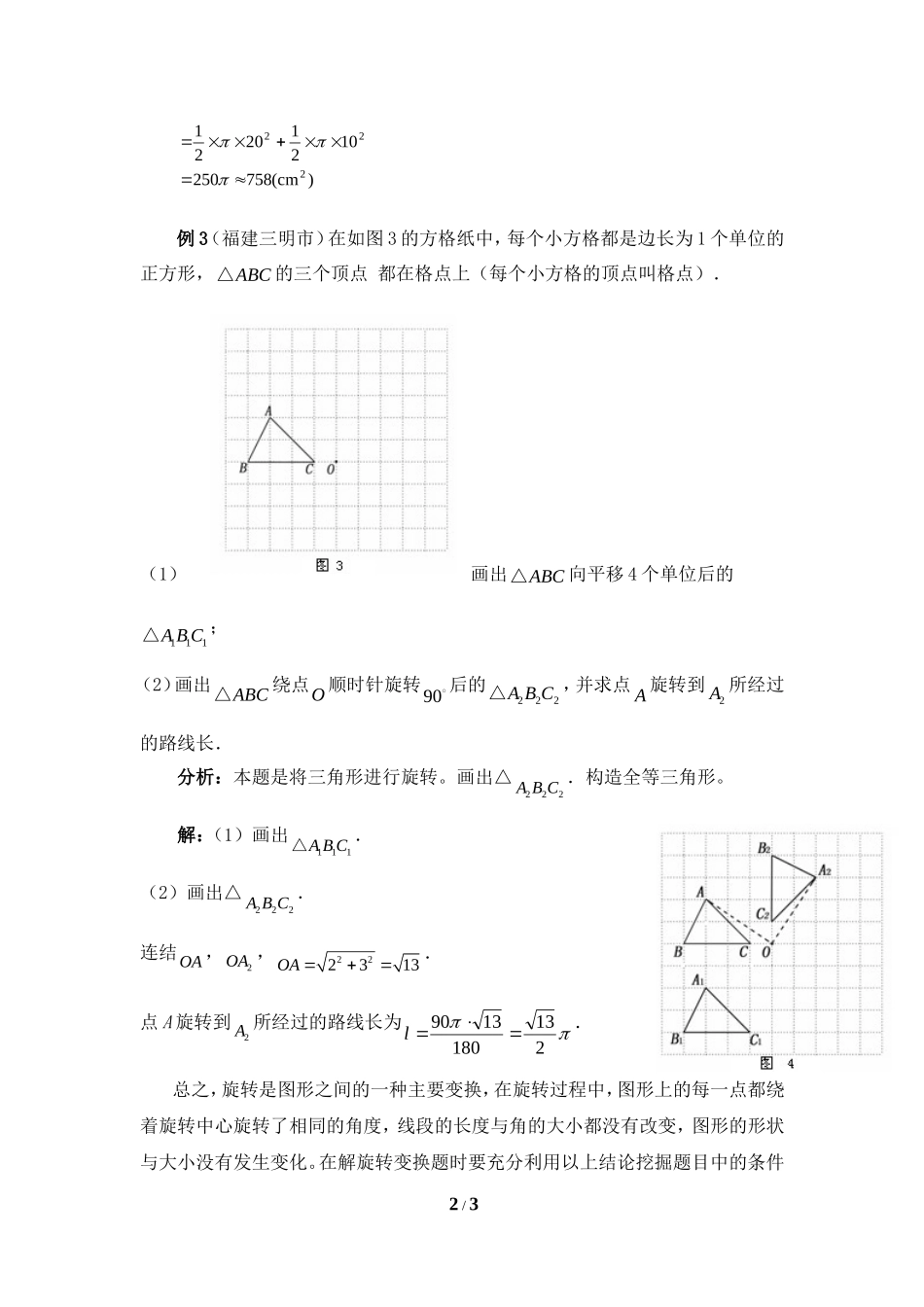
旋转中考创新题图形的旋转是新课标的重要内容,它既有利于考查学生的动手操作能力和空间思维能力,又培养了学生的创新意识和综合运用知识的能力,因此成为近年来中考命题的热点。列举几例一起来感受一下。例1.(扬州市)如图1,ABC△中(23)A,,(31)B,,(12)C,.(1)将ABC△向右平移4个单位长度,画出平移后的111ABC△;(2)画出ABC△关于x轴对称的222ABC△;(3)将ABC△绕原点O旋转180,画出旋转后的333ABC△;(4)在111ABC△,222ABC△,333ABC△中,△______与△______成轴对称,对称轴是______;△______与△______成中心对称,对称中心的坐标是______.解:图略(4)222ABC△与333ABC△成轴对称,对称轴是y轴.333ABC△与111ABC△成中心对称,对称中心的坐标是(20),.点评:此类题以格点网络为背景,通过三角形的平移、旋转考查学生发散思维的能力,本题有利于激发学生探究新问题的兴趣,还以亲切自然的语气引导学生进入活动情景,无疑是一道课改好题。例2(安阳)如图2,半圆M的直径AB为20cm,现将半圆M绕着点A顺时针旋转180°。(1)请你画出旋转后半圆M的图形;(2)求出在整个旋转过程中,半圆M所扫过区域的面积(结果精确到1cm2)。分析:半圆M所扫过的区域是由半圆M和以A为圆心,AB长为半径的半圆两部分组成的,正确找出这样的区域是解题的关键。解:(1)画图略。(2)半圆M所扫过的面积1/3)cm(75825010212021222例3(福建三明市)在如图3的方格纸中,每个小方格都是边长为1个单位的正方形,ABC△的三个顶点都在格点上(每个小方格的顶点叫格点).(1)画出ABC△向平移4个单位后的111ABC△;(2)画出ABC△绕点O顺时针旋转90后的222ABC△,并求点A旋转到2A所经过的路线长.分析:本题是将三角形进行旋转。画出△222ABC.构造全等三角形。解:(1)画出111ABC△.(2)画出△222ABC.连结OA,2OA,222313OA.点A旋转到2A所经过的路线长为2131801390l.总之,旋转是图形之间的一种主要变换,在旋转过程中,图形上的每一点都绕着旋转中心旋转了相同的角度,线段的长度与角的大小都没有改变,图形的形状与大小没有发生变化。在解旋转变换题时要充分利用以上结论挖掘题目中的条件2/3练习题:如图5,梯形ABCD中,DCAB,EF是中位线,ABEG于G,ABFH于H,梯形的高)(21DCABh.沿着HFGE,分别把AGE,BHF剪开,然后按图中箭头所指方向,分别绕着点E,F旋转0180,将会得到一个什么样的四边形?简述理由.答案:将会得到四边形HGHG一个正方形,理由略。3/3