59正弦定理、余弦定理(一）VIP免费

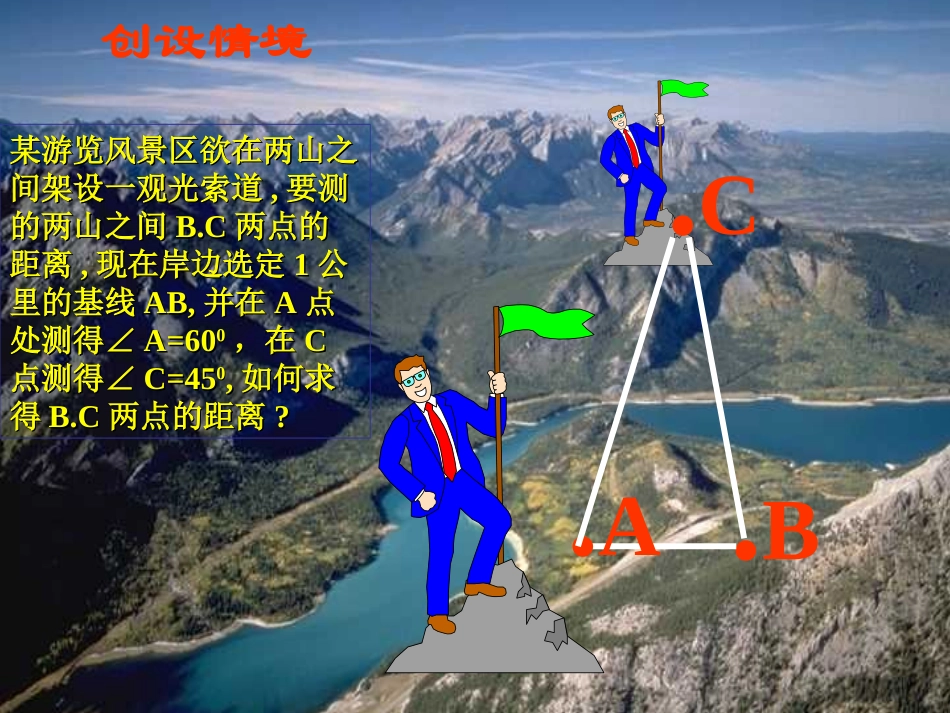
5.9正弦定理、余弦定理(一）25年1月15日教学目标：⑴掌握正弦定理⑵能应用正弦定理解斜三角形，解决实际问题。教学重点：正弦定理教学难点：正弦定理的正确理解和熟练运用创设情境.B.A某游览风景区欲在两山之某游览风景区欲在两山之间架设一观光索道间架设一观光索道,,要测要测的两山之间的两山之间B.CB.C两点的两点的距离距离,,现在岸边选定现在岸边选定11公公里的基线里的基线AB,AB,并在并在AA点点处测得∠处测得∠A=60A=6000，在，在CC点测得∠点测得∠C=45C=4500,,如何求如何求得得B.CB.C两点的距离两点的距离??.C解：过点B作BD⊥AC交AC点D在Rt△ADB中，sinA=DB=ABsinA在Rt△CDB中，sinC=DB=BCsinCABsinA=BCsinC，即ABDBBCDBABCcABsinsin0060sin45sin1BC26BCCABDCABBACsinsinBbAaCcsinsinsin复习引入回忆一下直角三角形的边角关系?ABCcba222cbaAcasinBcbsinAbatan90BA两等式间有联系吗？cBbAasinsin1sinCCcBbAasinsinsin这就是正弦定理，定理对直角三角形成立．对于锐角和钝角三角形，这一结论是否也成立呢？探究：jACB在锐角中，过A作单位向量j垂直于，ACABC则有j与的夹角为，j与的夹角为.等式A90CBC90ABCBACAB怎样建立三角形中边和角间的关系？ABjCBACj)()90cos()90cos(90cosAABjCCBjACjAcCasinsin即CcAasinsin同理，过C作单位向量j垂直于，可得CBCcBbsinsin新课教学：CcBbAasinsinsin在钝角三角形中，它的证明又如何呢？jACB在钝角中，过A作单位向量j垂直于，ACABC则有j与的夹角为，j与的夹角为.等式.90ACBC90ABCBACAB同样可证得：CcBbAasinsinsinCcBbAasinsinsin正弦定理在一个三角形中，各边和它所对角的正弦的比相等，即正弦定理可以解什么类型的三角形问题？已知两角和任意一边，可以求出其他两边和一角；已知两边和其中一边的对角，可以求出三角形的其他的边和角.2sinsinsinabcRABC（R为△ABC外接圆半径）已知a,b和A,用正弦定理求B时的各种情况:⑴若A为锐角时:)(ba),(babsinA)(bsinAasin锐角一解一钝一锐二解直角一解无解Abababababaa已知边a,b和A仅有一个解有两个解仅有一个解无解abCH=bsinA