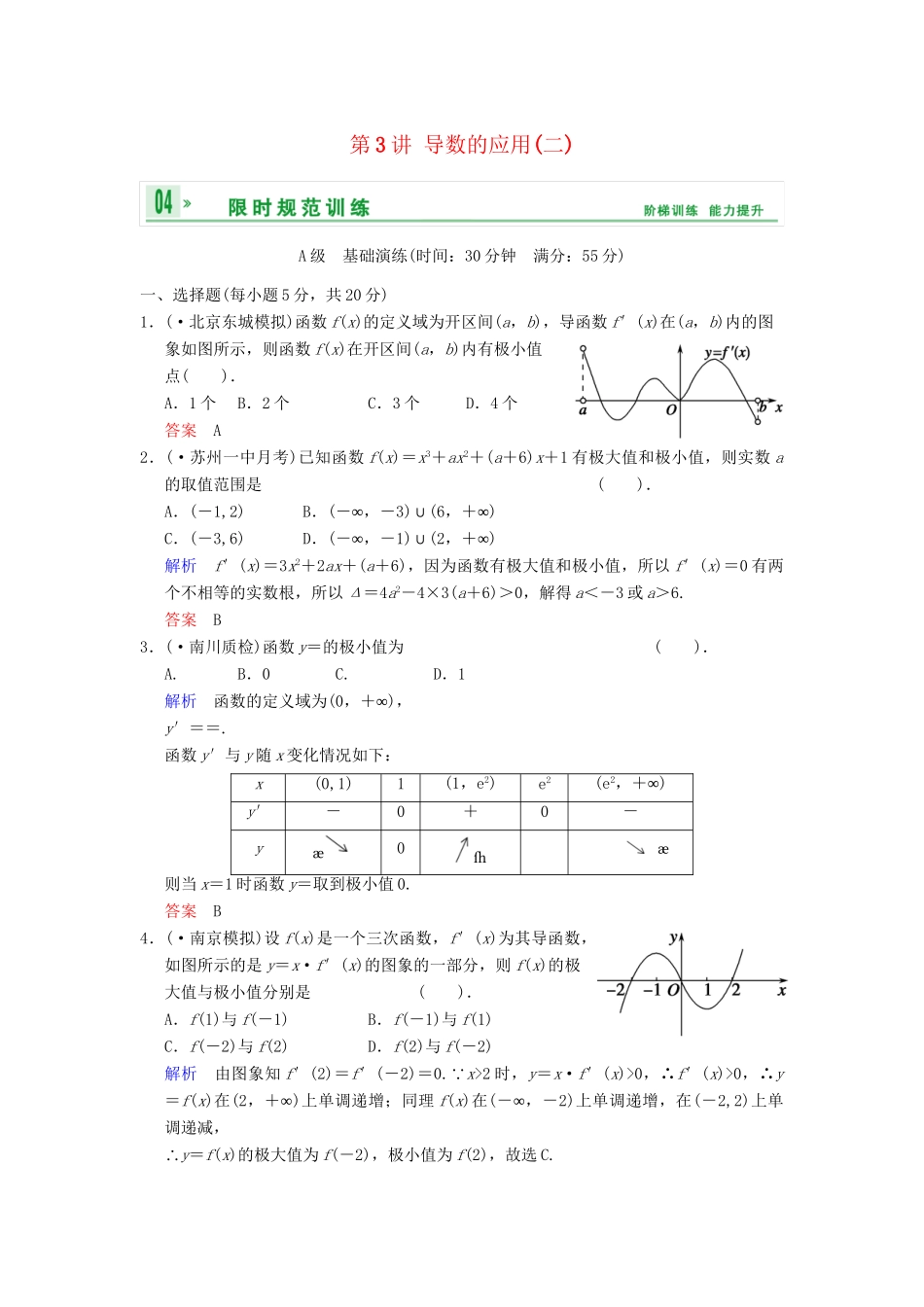
第3讲导数的应用(二)A级基础演练(时间:30分钟满分:55分)一、选择题(每小题5分,共20分)1.(·北京东城模拟)函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点().A.1个B.2个C.3个D.4个答案A2.(·苏州一中月考)已知函数f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则实数a的取值范围是().A.(-1,2)B.(∞-,-3)∪(6∞,+)C.(-3,6)D.(∞-,-1)∪(2∞,+)解析f′(x)=3x2+2ax+(a+6),因为函数有极大值和极小值,所以f′(x)=0有两个不相等的实数根,所以Δ=4a2-4×3(a+6)>0,解得a<-3或a>6.答案B3.(·南川质检)函数y=的极小值为().A.B.0C.D.1解析函数的定义域为(0∞,+),y′==.函数y′与y随x变化情况如下:x(0,1)1(1,e2)e2(e2∞,+)y′-0+0-y0则当x=1时函数y=取到极小值0.答案B4.(·南京模拟)设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x·f′(x)的图象的一部分,则f(x)的极大值与极小值分别是().A.f(1)与f(-1)B.f(-1)与f(1)C.f(-2)与f(2)D.f(2)与f(-2)解析由图象知f′(2)=f′(-2)=0. x>2时,y=x·f′(x)>0,∴f′(x)>0,∴y=f(x)在(2∞,+)上单调递增;同理f(x)在(∞-,-2)上单调递增,在(-2,2)上单调递减,∴y=f(x)的极大值为f(-2),极小值为f(2),故选C.答案C二、填空题(每小题5分,共10分)5.已知函数y=f(x)=x3+3ax2+3bx+c在x=2处有极值,其图象在x=1处的切线平行于直线6x+2y+5=0,则f(x)极大值与极小值之差为________.解析 y′=3x2+6ax+3b,⇒∴y′=3x2-6x,令3x2-6x=0,则x=0或x=2.∴f(x)极大值-f(x)极小值=f(0)-f(2)=4.答案46.已知函数f(x)=(其中e为自然对数的底数,且e≈2.718).若f(6-a2)>f(a),则实数a的取值范围是________.解析 f′(x)=当x≤e时,f′(x)=6-2x=2(3-x)>0,当x>e时,f′(x)=1-=>0,∴f(x)在R上单调递增.又f(6-a2)>f(a),∴6-a2>a,解之得-3