高考数学 最新专题冲刺 立体几何（2） 理VIP免费

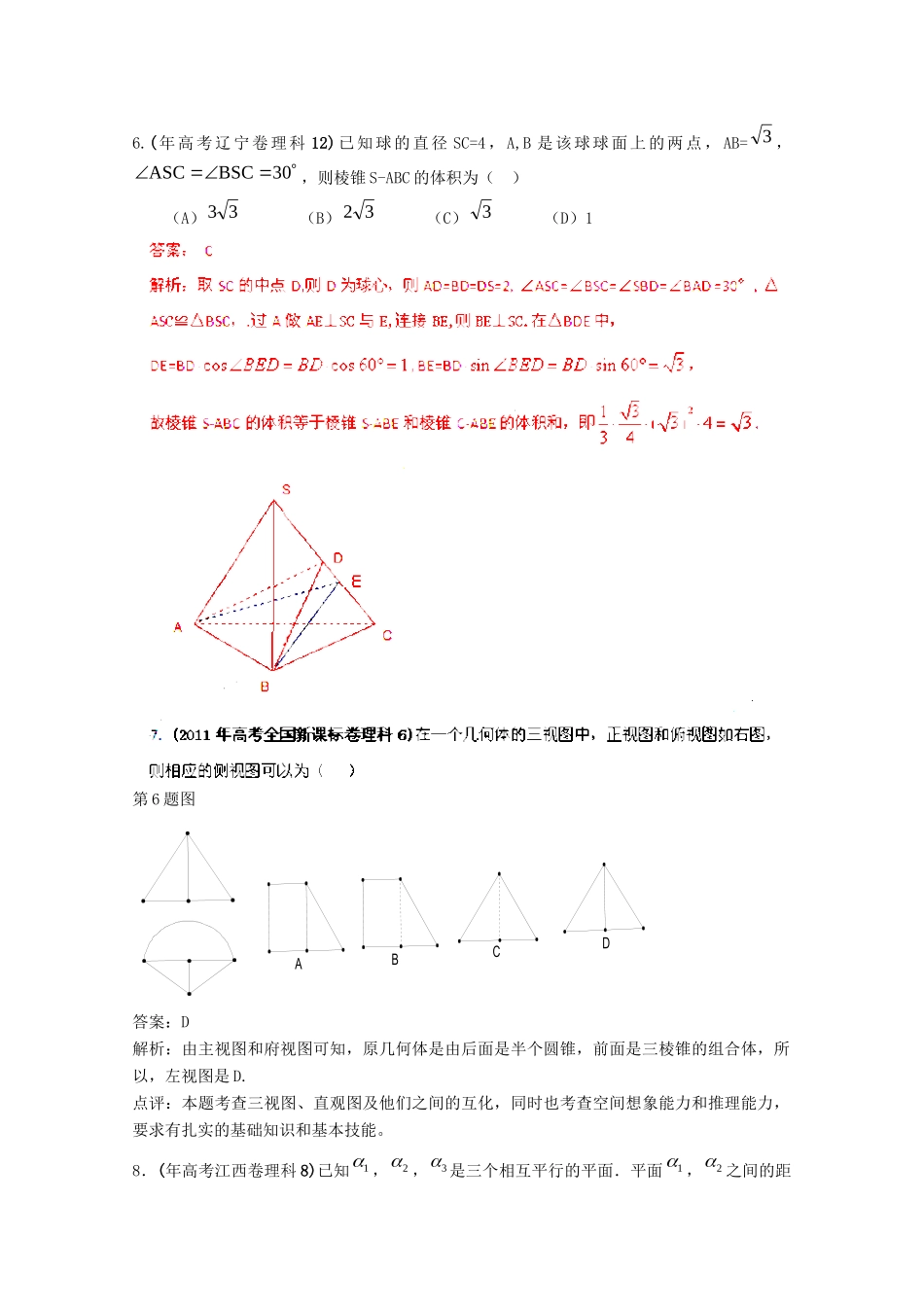
【备战】高考数学最新专题冲刺立体几何（2）理一、选择题:1.(年高考山东卷理科11)下图是长和宽分别相等的两个矩形．给定下列三个命题：①存在三棱柱，其正(主)视图、俯视图如下图；②存在四棱柱，其正(主)视图、俯视图如下图；③存在圆柱，其正(主)视图、俯视图如下图．其中真命题的个数是(A)3(B)2(C)1(D)0【答案】A【解析】对于①,可以是放倒的三棱柱；容易判断②③可以.2.(年高考浙江卷理科3)若某几何体的三视图如图所示，则这个几何体的直观图可以是4.(年高考安徽卷理科6)一个空间几何体得三视图如图所示，则该几何体的表面积为（A）48(B)32+8(C)48+8(D)80【答案】C【命题意图】本题考查三视图的识别以及空间多面体表面积的求法.【解析】由三视图可知几何体是底面是等腰梯形的直棱柱.底面等腰梯形的上底为2，下底为4，高为4，。故S表【解题指导】：三视图还原很关键，每一个数据都要标注准确。5.(年高考辽宁卷理科8)如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD，则下故AC⊥平面ABD,因为SB平面ABD,所以AC⊥SB，正确.对于B：因为AB//CD,所以AB//平面SCD.对于C:设ACBDO.因为AC⊥平面ABD，所以SA和SC在平面SBD内的射影为SO，则∠ASO和∠CSO就是SA与平面SBD所成的角和SC与平面SBD所成的角，二者相等，正确.故选D.6.(年高考辽宁卷理科12)已知球的直径SC=4，A,B是该球球面上的两点，AB=3，30BSCASC，则棱锥S-ABC的体积为（）（A）33（B）32（C）3（D）1第6题图答案：D解析：由主视图和府视图可知，原几何体是由后面是半个圆锥，前面是三棱锥的组合体，所以，左视图是D.点评：本题考查三视图、直观图及他们之间的互化，同时也考查空间想象能力和推理能力，要求有扎实的基础知识和基本技能。8．(年高考江西卷理科8)已知1，2，3是三个相互平行的平面．平面1，2之间的距ABCD332正视图侧视图俯视图图1离为1d，平面2，3之间的距离为2d．直线l与1，2，3分别相交于1P，2P，3P，“那么12PP=23PP”“是12dd”的A.充分不必要条件B.必要不充分条件C．充分必要条件D．既不充分也不必要条件【答案】C【解析】过点1P作平面2的垂线g,交平面2，3分别于点A、B两点,由两个平面平行的性质可知2PA∥3PB,所以121122PPdPPd,故选C.9.(年高考湖南卷理科3)设图1是某几何体的三视图，则该几何体的体积为A.1229B.1829C.429D.1836答案：B解析：由三视图可以还原为一个底面为边长是3的正方形，高为2的长方体以及一个直径为3的球组成的简单几何体，其体积等于233)23(3431829。故选B评析：本小题主要考查球与长方体组成的简单几何体的三视图以及几何体的体积计算.11.(年高考陕西卷理科5)某几何体的三视图如图所示，则它的体积是（A）283（B）83（C）82（D）23【答案】A【解析】：由三视图可知该几何体为立方体与圆锥，立方体棱长为2，圆锥底面半径为1、高为2，HGFEDCBA3123所以体积为3212123283故选A12.(年高考重庆卷理科9)高为24的四棱锥S-ABCD的底面是边长为1的正方形，点S、A、B、C、D均在半径为1的同一球面上，则底面ABCD的中心与顶点S之间的距离为（A）24（B）22（C）1（D）2解析：选C.设底面中心为G，球心为O，则易得22AG，于是22OG，用一个与ABCD所在平面距离等于24的平面去截球，S便为其中一个交点，此平面的中心设为H，则222244OH，故22227148SH，故22272184SGSHHG13．(年高考四川卷理科3)1l，2l，3l是空间三条不同的直线，则下列命题正确的是()(A)12ll，23ll13ll（B）12ll，23ll13ll(C)233lll1l，2l，3l共面（D）1l，2l，3l共点1l，2l，3l共面【答案】C【解析】如图，作DEBC于E，由l为直二面角，ACl，得AC平面，进而ACDE,又BCDE,BCACC,于是DE平面ABC。故DE为D到平面ABC的距离。在RtBCD中，利用等面积法得126.33BDDCDEBClβαABCDE15.(年高考全国卷理科11)已知平面截一球面得圆M，...