北京大学附中版高考数学二轮复习 考前抢分必备专题训练 选考内容VIP免费

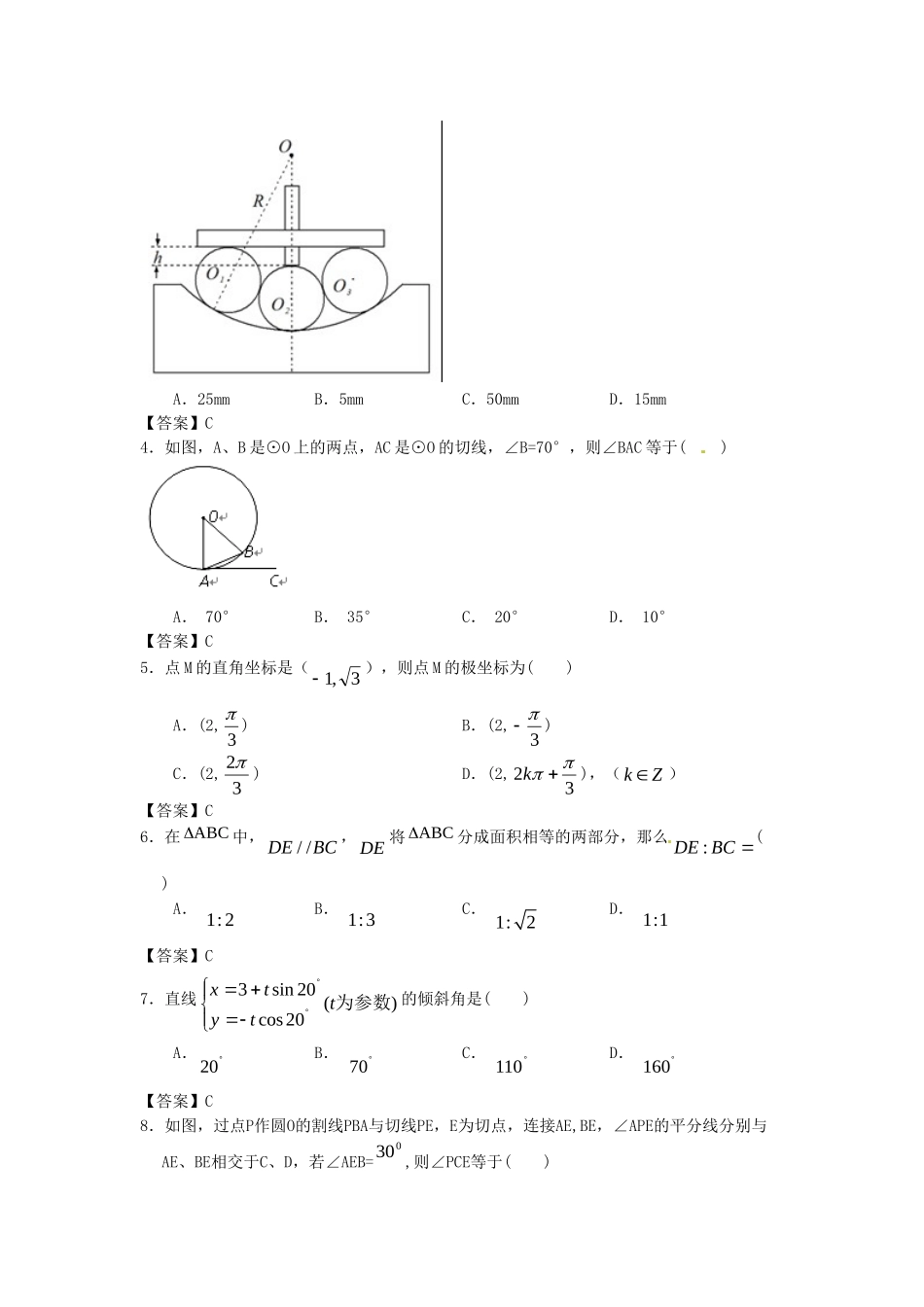
北京大学附中版《创新设计》高考数学二轮复习考前抢分必备专题训练：选考内容本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．在参数方程sincostbytax（t为参数）所表示的曲线上有B、C两点，它们对应的参数值分别为t1、t2，则线段BC的中点M对应的参数值是()A．122ttB．122ttC．122ttD．122tt【答案】B2．如图，AB为O的直径，弦AC，BD交于点P，若3,1ABCD，则sinAPD()A．63B．33C．13D．223【答案】D3．如图所示，为了测量该工件上面凹槽的圆弧半径R，由于没有直接的测量工具，工人用三个半径均为r（r相对R较小）的圆柱棒123,,OOO放在如图与工件圆弧相切的位置上，通过深度卡尺测出卡尺水平面到中间量棒2O顶侧面的垂直深度h，若10,4rmmhmm时，则R的值为()A．25mmB．5mmC．50mmD．15mm【答案】C4．如图，A、B是⊙O上的两点，AC是⊙O的切线，∠B=70°，则∠BAC等于()A．70°B．35°C．20°D．10°【答案】C5．点M的直角坐标是（3,1），则点M的极坐标为()A．(2,3)B．(2,3)C．(2,32)D．(2,32k)，（Zk）【答案】C6．在ABC中，//DEBC，DE将ABC分成面积相等的两部分，那么:DEBC()A．1:2B．1:3C．1:2D．1:1【答案】C7．直线)(20cos20sin3为参数ttytx的倾斜角是()A．20B．70C．110D．160【答案】C8．如图，过点P作圆O的割线PBA与切线PE，E为切点，连接AE,BE，∠APE的平分线分别与AE、BE相交于C、D，若∠AEB=030,则∠PCE等于()A.0150B.075C.0105D.060【答案】C9．直线l的极坐标方程为2cossin3，圆C的极坐标方程为22sin()4．则直线l和圆C的位置关系为()A．相交但不过圆心B．相交且过圆心C．相切D．相离【答案】A10．若点P(3,m)在以点F为焦点的抛物线244xtyt(t为参数)上,则|PF|等于()A．2B．3C．4D．5【答案】C11．曲线的极坐标方程sin4化为直角坐标为()A．4)2(22yxB．4)2(22yxC．4)2(22yxD．4)2(22yx【答案】B12．如图，E是平行四边形ABCD的边BC的延长线上的一点，连结AE交CD于F，则图中共有相似三角形()A．1对B．2对C．3对D．4对【答案】C第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．如图，PABPCD、为圆O的两条割线，若5PA，7AB，11CD，2AC，则BD等于．【答案】614．如图，PA是圆O的切线，A为切点，PBC是圆O的割线．若32PABC，则PBBC____________．【答案】1215．在极坐标系中，点(2,)3M到直线2:sin()42l的距离为____________【答案】6216．将参数方程sin2cos21yx（为参数）化为普通方程，所得方程是____________.【答案】4)1(22yx三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．已知曲线C的极坐标方程是cos4．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是tymtx2222（t是参数）．若l与C相交于AB两点，且14AB．(1）求圆的普通方程，并求出圆心与半径；(2）求实数m的值．【答案】（1）曲线C的极坐标方程化为直角坐标方程为2240xyx，圆心坐标为(2,0)，半径2R．(2）直线l的直角坐标方程为yxm，则圆心到直线l的距离21424()22d所以20222m，可得21m，解得1m或3m．18．如图，已知⊙O和⊙M相交于A、B两点，AD为⊙M的直径，直线BD交⊙O于点C，点G为BD中点，连结AG分别交⊙O、BD于点E、F连结CE．(1）求证：GDCEEFAG；(2）求证：.22CEEFAGGF【答案】（1）连结AB，AC， AD为M的直径，∴090ABD，∴AC为O的直径,∴CEFAGD, DFGCFE，∴ECFGDF, G为弧BD中点，∴DAGGDF， ECBBAG,∴DAGECF,∴CEF∽AGD，∴CEAGEFGD，GDCEEFAG(2）由（1）知DAGGDF...