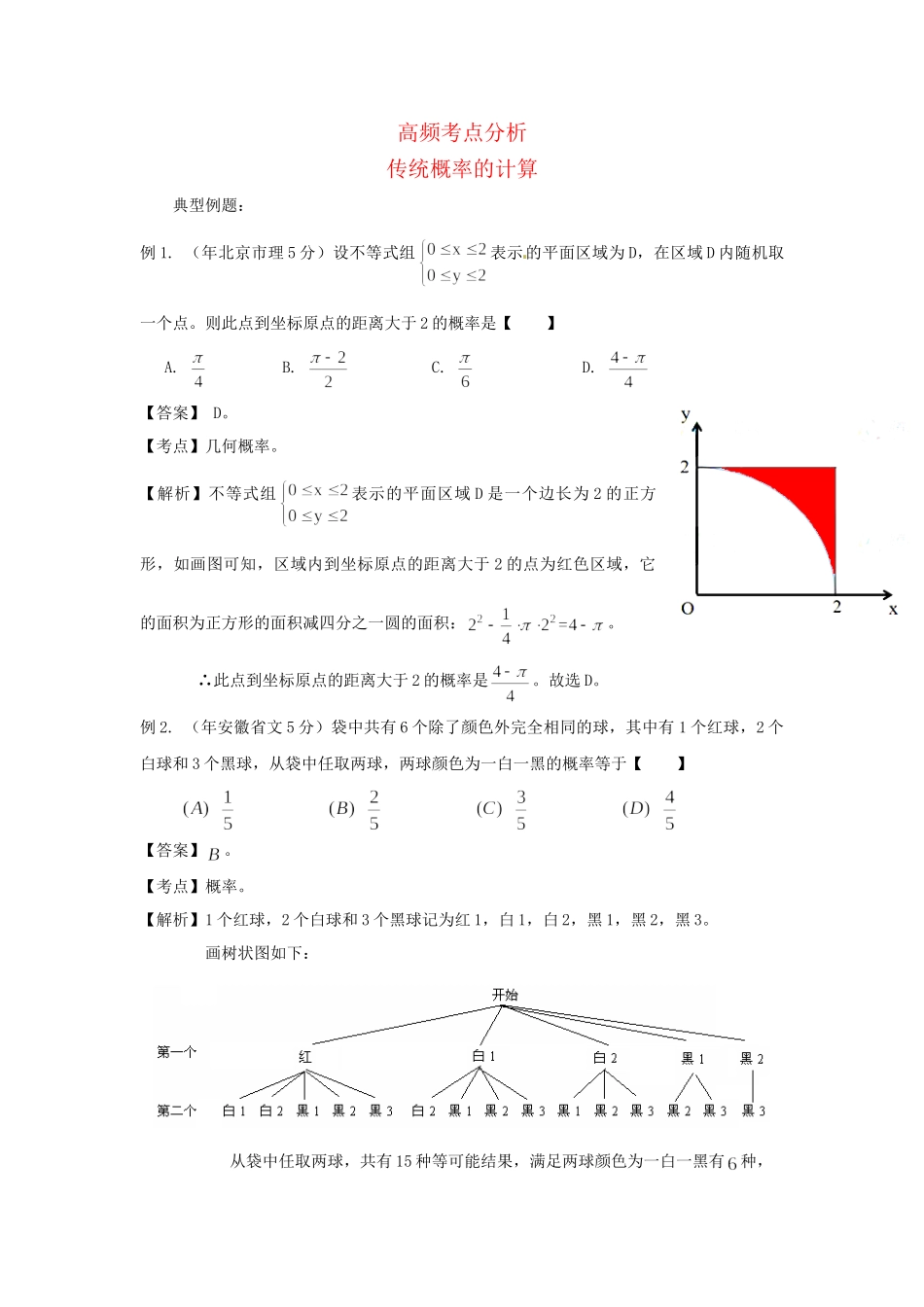
高频考点分析传统概率的计算典型例题:例1.(年北京市理5分)设不等式组表示的平面区域为D,在区域D内随机取一个点。则此点到坐标原点的距离大于2的概率是【】A.B.C.D.【答案】D。【考点】几何概率。【解析】不等式组表示的平面区域D是一个边长为2的正方形,如画图可知,区域内到坐标原点的距离大于2的点为红色区域,它的面积为正方形的面积减四分之一圆的面积:。∴此点到坐标原点的距离大于2的概率是。故选D。例2.(年安徽省文5分)袋中共有6个除了颜色外完全相同的球,其中有1个红球,2个白球和3个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于【】【答案】。【考点】概率。【解析】1个红球,2个白球和3个黑球记为红1,白1,白2,黑1,黑2,黑3。画树状图如下:从袋中任取两球,共有15种等可能结果,满足两球颜色为一白一黑有种,∴概率等于。故选。例3.(年广东省理5分)从概率位数与十位数之和为奇数的两位数中任取一个,其个位数为0的概率是【】A.B.C.D.【答案】D。【考点】分类讨论的思想,概率。【解析】由题意知,个位数与十位数应该一奇一偶。①个位数为奇数,十位数为偶数共有5×5=25个两位数;②个位数为偶数,十位数为奇数共有5×4=20个两位数。两类共有25+20=45个数,其中个位数为0,十位数为奇数的有10,30,50,70,90共5个数。∴概率位数为0的概率是=。故选D。例4.(年湖北省理5分)如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆。在扇形OAB内随机取一点,则此点取自阴影部分的概率是【】A.B.C.D.【答案】A。【考点】概率,扇形面积,特殊元素法。【解析】取大圆的半径为2,则小圆半径为1,如图,两个半圆相交的阴影部分是两个弓形,连接OC,取OA的中点D,连接CD。∴两个半圆相交的阴影部分面积为。又 扇形OAB的面积为,∴阴影部分的面积为。在扇形OAB内随机取一点,则此点取自阴影部分的概率。故选A。例5.(年福建省理5分)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为【】A.B.C.D.【答案】C。【考点】定积分的计算,几何概型的计算。【解析】 ,∴利用几何概型公式得:。故选C。例6.(年辽宁省理5分)在长为12cm的线段AB上任取一点C.现作一矩形,领边长分别等于线段AC,CB的长,则该矩形面积小于32cm2的概率为【】(A)(B)(C)(D)【答案】C。【考点】函数模型的应用、不等式的解法、几何概型的计算。【解析】设线段AC的长为cm,则线段CB的长为()cm。那么矩形的面积为cm2。由,解得。又,所以该矩形面积小于32cm2的概率为。故选C。例7.(年辽宁省文5分)在长为12cm的线段AB上任取一点C.现作一矩形,邻边长分别等于线段AC,CB的长,则该矩形面积大于20cm2的概率为【】:(A)(B)(C)(D)【答案】C。【考点】函数模型的应用、不等式的解法、几何概型的计算【解析】设线段AC的长为cm,则线段CB的长为()cm,那么矩形的面积为cm2,由,解得。又,所以该矩形面积大于20cm2的概率为。故选C。例8.(年上海市文4分)三位同学参加跳高、跳远、铅球项目的比赛,若每人都选择其中两个项目,则有且仅有两人选择的项目完全相同的概率是▲(结果用最简分数表示).【答案】。【考点】排列组合概率问题(古典概型)。【解析】设概率,则。求k,分三步:①选二人,让他们选择的项目相同,有种;②确定上述二人所选择的相同的项目,有种;③确定另一人所选的项目,有种.所以,故。例9.(年湖南省理5分)函数的导函数的部分图像如图所示,其中,P为图像与y轴的交点,A,C为图像与轴的两个交点,B为图像的最低点.(1)若,点P的坐标为,则▲;(2)若在曲线段与轴所围成的区域内随机取一点,则该点在△ABC内的概率为▲.【答案】(1)3;(2)。【考点】三角函数的图像与性质,定积分,几何概率。【解析】(1),当,点P的坐标为时,,∴。(2)由图知,。 ,∴曲线段与轴所围成的区域面积为。由几何概率知该点在△ABC内的概率为。例10.(年浙江省文5分)从边长为1的正方形的中心和顶点这五点中,随机(等可能)取两点,则该两点间的距离为的概率是▲。【答案】。【考点】随机事件的概率。【解析】从边长为1的正方形的中心和顶点这五点中,...