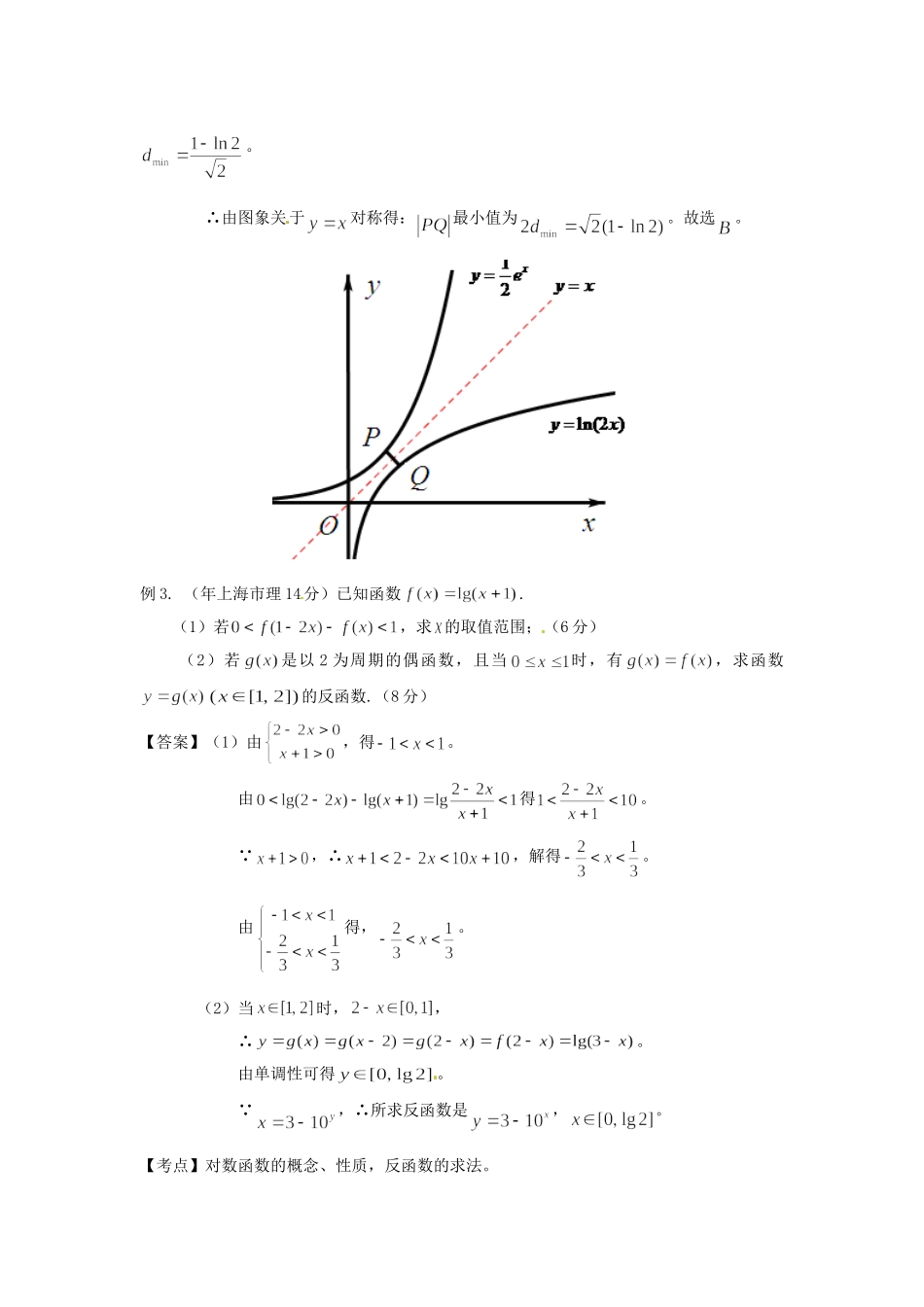
反函数问题典型例题:例1.(年全国大纲卷文5分)函数=(≥-1)的反函数为【】A.B.C.D.【答案】A。【考点】反函数。【解析】由原函数求出关于的关系式,再、对换,原函数的值域是反函数的定义域。因此,将=两边平方,得,即。将、对换,得。又函数=的值域为,所以的定义域为。故选A。例2.(年全国课标卷理5分)设点在曲线上,点在曲线上,则最小值为【】【答案】。【考点】反函数的性质,导数的应用。【解析】∵函数与函数互为反函数,∴它们的图象关于对称。∴函数上的点到直线的距离为设函数,则,∴。∴。∴由图象关于对称得:最小值为。故选。例3.(年上海市理14分)已知函数.(1)若,求的取值范围;(6分)(2)若是以2为周期的偶函数,且当时,有,求函数的反函数.(8分)【答案】(1)由,得。由得。∵,∴,解得。由得,。(2)当时,,∴。由单调性可得。∵,∴所求反函数是,。【考点】对数函数的概念、性质,反函数的求法。【解析】(1)由,结合对数函数的性质,列不等式组求解即可。(2)根据对数函数与指数函数互为反函数的性质求解。