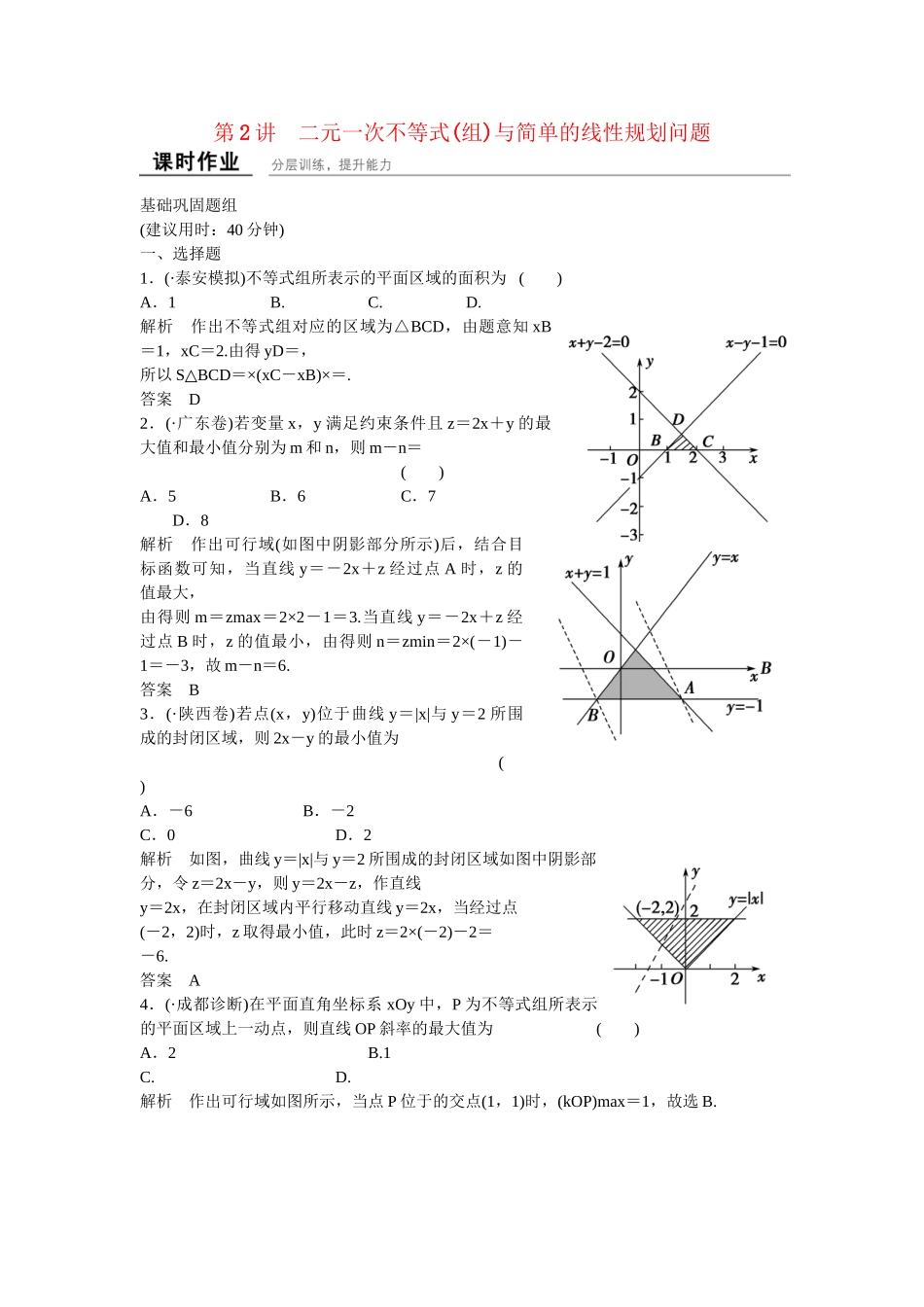
第2讲二元一次不等式(组)与简单的线性规划问题基础巩固题组(建议用时:40分钟)一、选择题1.(·泰安模拟)不等式组所表示的平面区域的面积为()A.1B.C.D.解析作出不等式组对应的区域为△BCD,由题意知xB=1,xC=2.由得yD=,所以SBCD△=×(xC-xB)×=.答案D2.(·广东卷)若变量x,y满足约束条件且z=2x+y的最大值和最小值分别为m和n,则m-n=()A.5B.6C.7D.8解析作出可行域(如图中阴影部分所示)后,结合目标函数可知,当直线y=-2x+z经过点A时,z的值最大,由得则m=zmax=2×2-1=3.当直线y=-2x+z经过点B时,z的值最小,由得则n=zmin=2×(-1)-1=-3,故m-n=6.答案B3.(·陕西卷)若点(x,y)位于曲线y=|x|与y=2所围成的封闭区域,则2x-y的最小值为()A.-6B.-2C.0D.2解析如图,曲线y=|x|与y=2所围成的封闭区域如图中阴影部分,令z=2x-y,则y=2x-z,作直线y=2x,在封闭区域内平行移动直线y=2x,当经过点(-2,2)时,z取得最小值,此时z=2×(-2)-2=-6.答案A4.(·成都诊断)在平面直角坐标系xOy中,P为不等式组所表示的平面区域上一动点,则直线OP斜率的最大值为()A.2B.1C.D.解析作出可行域如图所示,当点P位于的交点(1,1)时,(kOP)max=1,故选B.答案B5.(·济南模拟)已知变量x,y满足约束条件目标函数z=x+2y的最大值为10,则实数a的值为()A.2B.C.4D.8解析结合图形求解.作出不等式组对应的平面区域,当目标函数经过点(a,a-1)时取得最大值10,所以a+2(a-1)=10,解得a=4,故选C.答案C二、填空题6.(·日照调研)若A为不等式组表示的平面区域,则当a从-2连续变化到1时,动直线x+y=a扫过A中的那部分区域的面积为________.解析平面区域A如图所示,所求面积为S=×2×2-××=2-=.答案7.在平面直角坐标系xOy中,M为不等式组所表示的区域上一动点,则|OM|的最小值是________.解析如图所示阴影部分为可行域,数形结合可知,原点O到直线x+y-2=0的垂线段长是|OM|的最小值,|OM|min∴==.答案8.(·盐城调研)设x,y满足约束条件若目标函数z=abx+y(a>0,b>0)的最大值为35,则a+b的最小值为________.解析可行域如图所示,当直线abx+y=z(a>0,b>0)过点B(2,3)时,z取最大值2ab+3,于是有2ab+3=35,ab=16,所以a+b≥2=2=8,当且仅当a=b=4时等号成立,所以(a+b)min=8.答案8三、解答题9.(·合肥模拟)画出不等式组表示的平面区域,并回答下列问题:(1)指出x,y的取值范围;(2)平面区域内有多少个整点?解(1)不等式组表示的平面区域如图所示.结合图中可行域得x∈,y∈[-3,8].(2)由图形及不等式组知当x=3时,-3≤y≤8,有12个整点;当x=2时,-2≤y≤7,有10个整点;当x=1时,-1≤y≤6,有8个整点;当x=0时,0≤y≤5,有6个整点;当x=-1时,1≤y≤4,有4个整点;当x=-2时,2≤y≤3,有2个整点;∴平面区域内的整点共有2+4+6+8+10+12=42(个).10.制订投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%.若投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?解设投资人分别用x万元,y万元投资甲、乙两个项目,由题意知目标函数z=x+0.5y.上述不等式组表示的平面区域如图所示,阴影部分(含边界)即为可行域.将z=x+0.5y变形为y=-2x+2z,这是斜率为-2随z变化的一组平行线,当直线y=-2x+2z经过可行域内的点M时,直线y=-2x+2z在y轴上的截距2z最大,z也最大.这里M点是直线x+y=10和0.3x+0.1y=1.8的交点.解方程组得x=4,y=6,此时z=4+0.5×6=7(万元).∴当x=4,y=6时,z取得最大值,所以投资人用4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8万元的前提下,使可能的盈利最大.能力提升题组(建议用时:25分钟)11.已知圆C:(x-a)2+(y-b)2=1,平面区域Ω:若圆心C∈Ω,且圆C与x轴相切,则a2+b2的最大值为()A.5B.29C.37D...