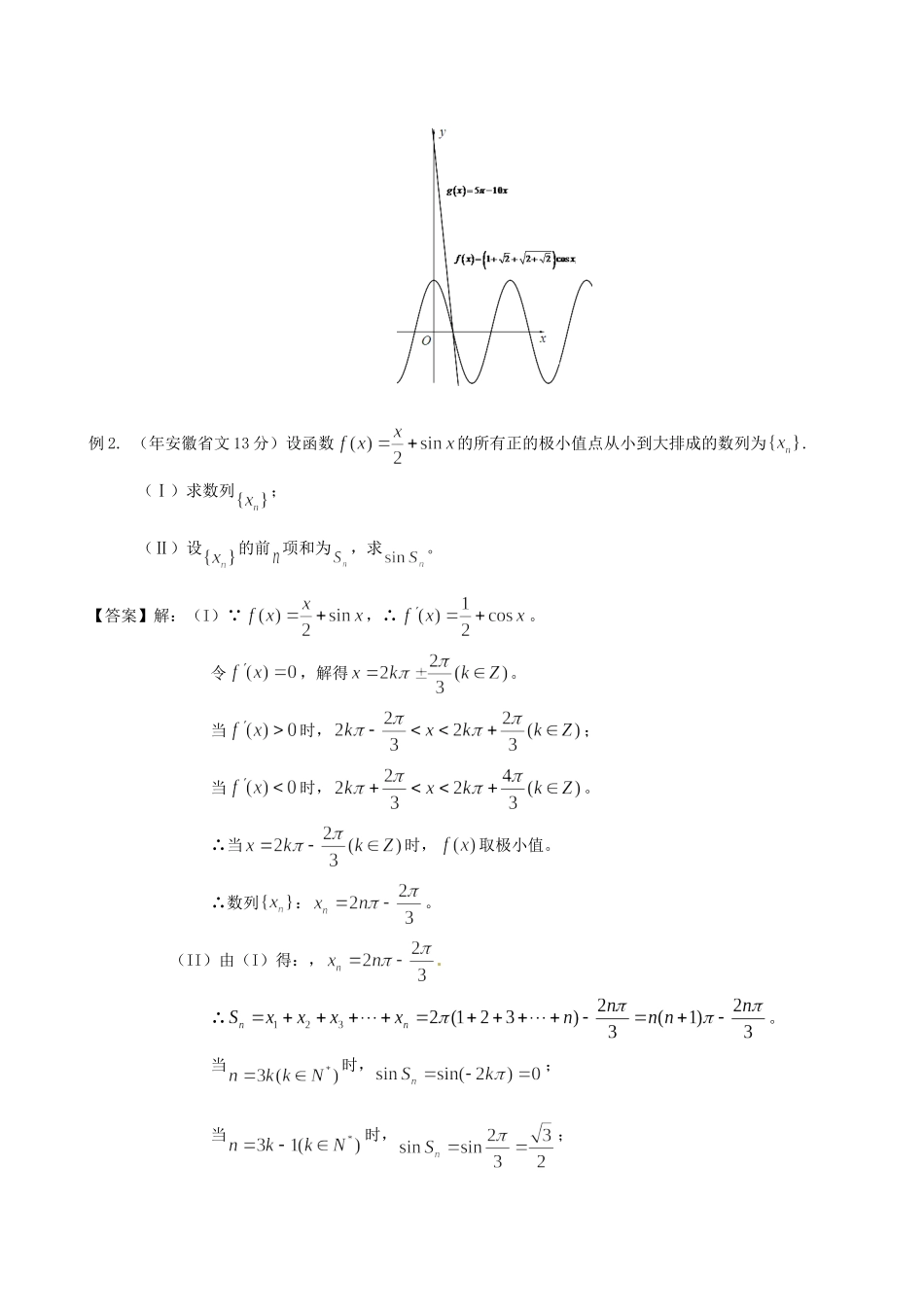
数列与三角函数的综合应用数列与三角函数的结合是一类创新试题,利用三角函数的周期性体现数列的变化。典型例题:例1.(年四川省理5分)设函数,是公差为的等差数列,,则【】A、B、C、D、【答案】D。【考点】等差数列性质,三角函数性质。【解析】∵,,∴。∵是公差为的等差数列,∴,。∴,解得。∴。故选D。关于,可化为。由,设,作图可得二者交点在处:例2.(年安徽省文13分)设函数的所有正的极小值点从小到大排成的数列为.(Ⅰ)求数列;(Ⅱ)设的前项和为,求。【答案】解:(I)∵,∴。令,解得。当时,;当时,。∴当时,取极小值。∴数列:。(II)由(I)得:,∴。当时,;当时,;当时,。∴当时,;当时,;当时,。【考点】三角函数的极值,导数的应用,数列。【解析】(I)求函数的所有正的极小值点,即要讨论,和的情况,得出结果。(II)求出的前项和为,分类讨论,求出。例3.(年全国大纲卷文10分)中,内角、、成等差数列,其对边、、满足,求A.【答案】解:∵中,内角、、成等差数列,∴。∴,。又∵,∴根据正弦定理,得。∴。“由”进行均值换元,设,。则,化简,得。∴。∴或。【考点】解三角形的运用,等差数列的性质,三角形的内角和定理,正弦定理,两角和的三角函数。【解析】根据角、、成等差数列和三角形内角和定理可得,。运用均值换元法,由应用正弦定理和两角和的三角函数,化简等式,求出答案。例4.(年山东省文12分)在△ABC中,内角A,B,C所对的边分别为,已知.(Ⅰ)求证:成等比数列;(Ⅱ)若,求△ABC的面积S.【答案】解:(Ⅰ)由已知得:,即。∵,∴。由正弦定理,得,∴成等比数列。(Ⅱ)若,则,由余弦定理,得,∴。∴△ABC的面积。【考点】正弦定理和余弦定理的应用,和的三角函数公式,同角三角函数公式,等比数列的判定。【解析】(Ⅰ)根据和的三角函数公式化简,求得三角正弦之间的关系,由正弦定理推出结论。[(Ⅱ)由余弦定理求出的余弦,从而根据同角三角函数公式得到正弦,应用面积公式求解。例5.(年辽宁省文12分)在中,角A、B、C的对边分别为a,b,c。角A,B,C成等差数列。(Ⅰ)求的值;(Ⅱ)边a,b,c成等比数列,求的值。【答案】解:(Ⅰ)∵角A,B,C成等差数列,∴。又∵,∴=60°。∴。(Ⅱ)∵边a,b,c成等比数列,∴。∴根据正弦定理得。∵=60°,∴。∴。【考点】数列与三角函数的综合,正弦定理、余弦定理、三角形内角和定理及等差、等比数列的定义。【解析】(Ⅰ)在中,由角A、B、C成等差数列可知B=60°,从而可得的值。(Ⅱ)由a,b,c成等比数列,得,由的值得到的值,结合正弦定理可求得的值。另解:由余弦定理求得得到是等边三角形,每个内角等于600求解。例6.(2012年上海市理5分)设25sin1nnan,nnaaaS21,在10021,,,SSS中,正数的个数是【】A.25B.50C.75D.100【答案】D。【考点】正弦函数的周期性。【解析】∵对于(只有),∴都为正数。当时,令,则,画出终边如右,其终边两两关于轴对称,即有,∴其中=26,27,…,49,此时。∵,,∴。从而当=26,27,…,49时,都是正数。又。同上可得,对于从51到100的情况同上可知都是正数,故选D。例7.(年福建省理4分)已知△ABC的三边长成公比为的等比数列,则其最大角的余弦值为▲.【答案】。【考点】等比数列的性质,余弦定理的应用。【解析】∵△ABC的三边长成公比为的等比数列,∴设三角形的三边分别是:a、a、a。∵最大角所对的边是a,∴根据三角形中大边对大角的性质,结合余弦定理得:。∴最大角的余弦值为。