广东省广州大学附中高考数学二轮简易通全套课时检测 导数及其应用 新人教版VIP免费

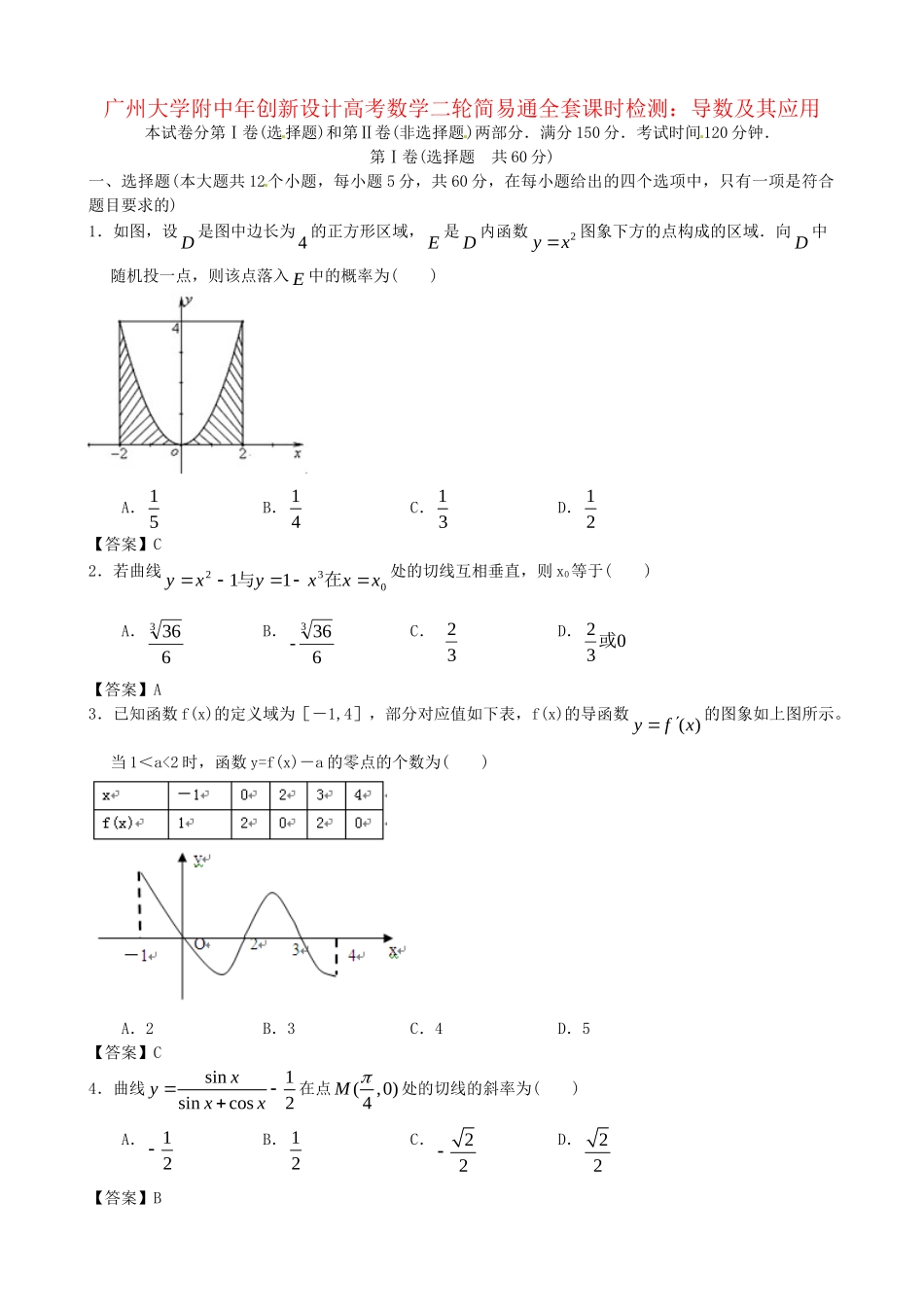
广州大学附中年创新设计高考数学二轮简易通全套课时检测：导数及其应用本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．如图，设D是图中边长为4的正方形区域，E是D内函数2yx图象下方的点构成的区域．向D中随机投一点，则该点落入E中的概率为()A．15B．14C．13D．12【答案】C2．若曲线03211xxxyxy在与处的切线互相垂直，则x0等于()A．6363B．636-3C．32D．032或【答案】A3．已知函数f(x)的定义域为［－1,4］，部分对应值如下表，f(x)的导函数()yfx的图象如上图所示。当1＜a<2时，函数y=f(x)－a的零点的个数为()A．2B．3C．4D．5【答案】C4．曲线sin1sincos2xyxx在点(,0)4M处的切线的斜率为()A．12B．12C．22D．22【答案】B5．220(1(1))axxdx的值是()A．143B．143C．123D．12【答案】A6．32()32fxaxx,若4)1(f,则a=()A．319B．316C．313D．310【答案】D7．若'0()2fx，则000()()lim2kfxkfxk等于()A．12B．12C．1D．2【答案】C8．函数3sin(,)32yx在点处的切线的斜率为()A．32B．22C．12D．1【答案】C9．由231yx，1,3xx及x轴围成的图形的面积为()A．28B．26C．30D．323【答案】A10．已知函数2()21fxx的图象上一点(1,1)及邻近一点,1(1)xy，则yx等于()A．4B．4xC．42xD．242x【答案】C11．设函数f（x）＝ax2＋b（a≠0），若30f（x）dx＝3f（x0），则x0＝()A．±1B．C．±D．2【答案】C12．已知点P(1,2)是曲线y=2x2上一点，则P处的瞬时变化率为()A．2B．4C．6D．21【答案】B第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．已知函数xf的导函数为xf'，且满足2'232xfxxf，则5'f。【答案】614．已知函数2()2(2)fxxxf,则函数)(xf的图象在点2,2f处的切线方程是.【答案】4x-y-8=015．曲线xxxy223与x轴所围成的图形的面积为．【答案】123716．20)sin3(dxxx=__________．【答案】1832三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．已知函数2()(2,)fxxaxaaxR，()xgxe，设函数)()()(xgxfx.(Ⅰ）当1a时，求)(x的单调区间；(Ⅱ）求()gx在点(0,1)处的切线与直线1x及曲线()gx所围成的封闭图形的面积；(Ⅲ）是否存在实数a，使)(x的极大值为3？若存在，求出a的值，若不存在，请说明理由．【答案】1）当221,()(1),'()()xxaxxxexexx时.'()0,01;'()0,10.xxxxx当时当时或∴()x的单调递增区间为（0，1），单调递减区间为：(,0)，(1,)(2）切线的斜率为0'(0)|1xxkge，∴切线方程为1yx.所求封闭图形面积为1121000111[(1)](1)()|22xxxSexdxexdxexxe.(3）22'()(2)()[(2)]xxxxxaeexaxaexax，令'()0,02xxxa得或.若2a，0)(x，则)(x在R上单调递减，不存在极大值，舍去；若2a,列表如下：由表可知，2()(2)(4)axaae极大设22()(4),'()(3)0aaaaeaae，∴()(,2)a在上是增函数，∴()(2)23a，即2(4)3aae，∴不存在实数a，使()x极大值为3.18．已知函数21()22fxaxx，()gxlnx.(1)如果函数()yfx在[1,)上是单调增函数，求a的取值范围；(2)是否存在实数0a，使得方程()()(21)gxfxax在区间1(,)ee内有且只有两个不相等的实数根？若存在，请求出a的取值范围；若不存在，请说明理由．【答案】（Ⅰ）当0a时，()2fxx在[1,)上是单调增函数，符合题意．当0a时，()yfx的对称轴方程为2xa，由于()yfx在[1,)上是单调增函数，所以21a，解得2a或0a，所以0a．当0a时，不符合题意．综上，a的取值...