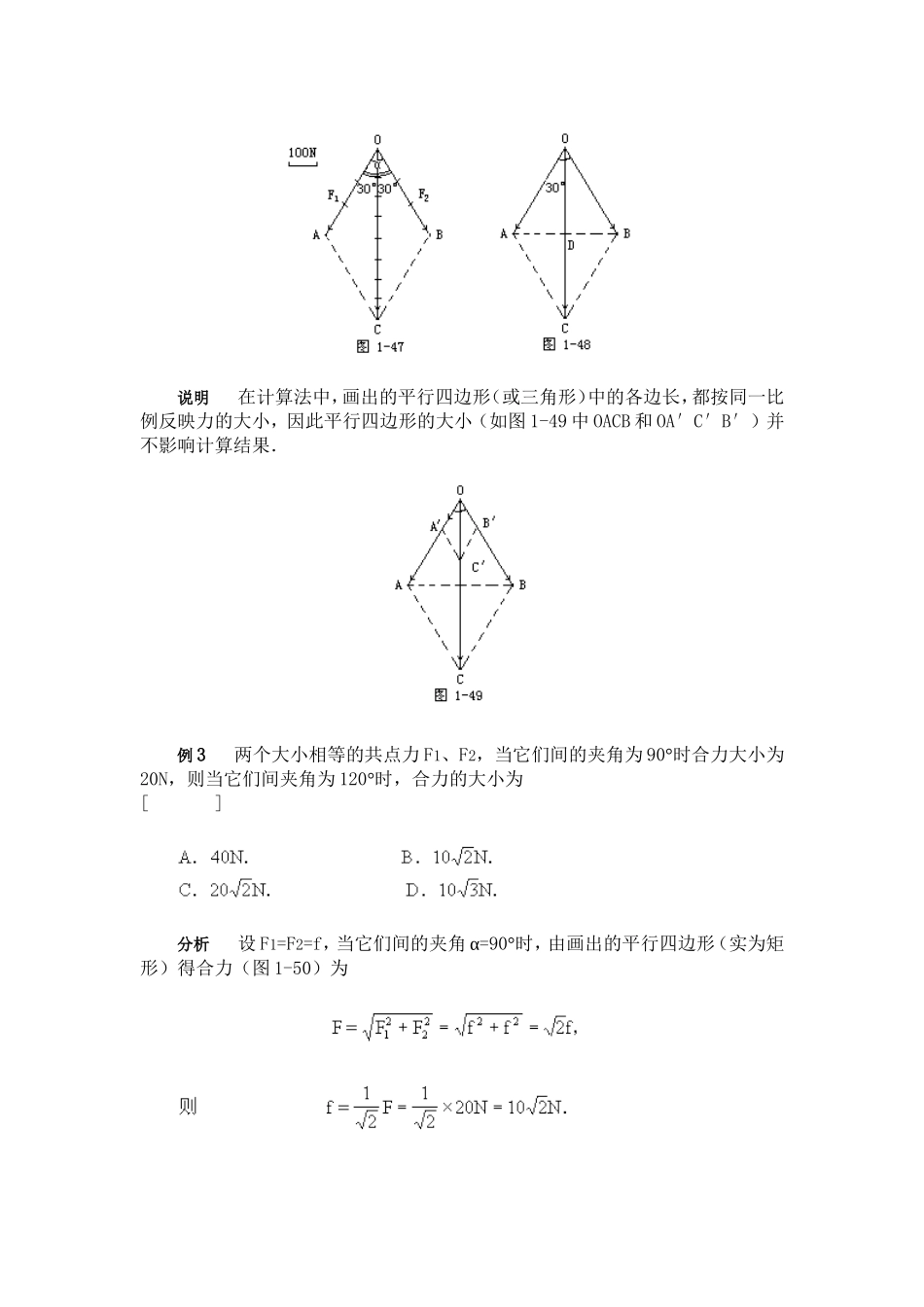
力的合成·典型题剖析例1互成角度的两个共点力,有关它们的合力和分力关系的下列说法中,正确的是[]A.合力的大小一定大于小的分力、小于大的分力.B.合力的大小随分力夹角的增大而增大.C.合力的大小一定大于任意一个分力.D.合力的大小可能大于大的分力,也可能小于小的分力.分析根据力的平行四边形法则可知,两个共点力的合力的大小不一定大于小的分力(图1-43)、小于大的分力(图1-44);合力的大小也不随夹角的增大而增大(图1-45);并且也不一定大于任意一个分力.答D.例2在电线杆的两侧常用钢丝绳把它固定在地上(图1-46).如果钢丝绳与地面的夹角∠A=∠B=60°,每条钢丝绳的拉力都是300N,求两根钢丝绳作用在电线杆上的合力.分析由图可知,两根钢丝绳的拉力F1、F2之间成60°角,根据平行四边形法则可以用图解法和计算法分别求出电线杆受到的合力.解答(1)图解法:自O点引两根有向线段OA和OB,相互间夹角α为60°,设每单位长为100N,则OA和OB的长度都是3个单位长度.作出平行四边形OACB,其对角线OC就代表两个拉力F1、F2的合力F.量得OC长为5.2个单位长度所以合力的大小F=5.2×100N=520N.用量角器量得∠AOC=∠BOC=30°,所以合力方向竖直向下(图1-47).(2)计算法:先画出力的平行四边形(图1-48),由于OA=OB,∠AOD=30°.因为在力的平行四边形中,各线段按照同一比例表示力的大小,所以合力说明在计算法中,画出的平行四边形(或三角形)中的各边长,都按同一比例反映力的大小,因此平行四边形的大小(如图1-49中OACB和OA′C′B′)并不影响计算结果.例3两个大小相等的共点力F1、F2,当它们间的夹角为90°时合力大小为20N,则当它们间夹角为120°时,合力的大小为[]分析设F1=F2=f,当它们间的夹角α=90°时,由画出的平行四边形(实为矩形)得合力(图1-50)为当两分力F1和F2间夹角变为α′=120°时,同理画出平行四边形(图1-51).由于每一半组成一个等边三角形,因此其合力F′=F1=F2=答B.说明由本题可以推知,三个大小相等、互成120°角的共点力的合力一定等于零(图1-52).此时每一个力一定与其他两个力的合力等值反向.讨论1.两共点力F1、F2成任意夹角α时的合力,可根据作出的平行四边形由余弦定理得(图1-53):设合力F与其中一个分力(如图1-53中F2)的夹角为θ,则课本练习五中题(3)、(4)、(5)都可根据上述合力的公式加以验算.2.求两个以上共点力的合力,可依次应用平行四边形法则,且与合成的先后顺序无关.利用三角形法则时,可先固定一个力,再把其他各个力平移、且依次首尾相接,最后连接始、末两端的有向线段同样表示合力,如图1-54所示.