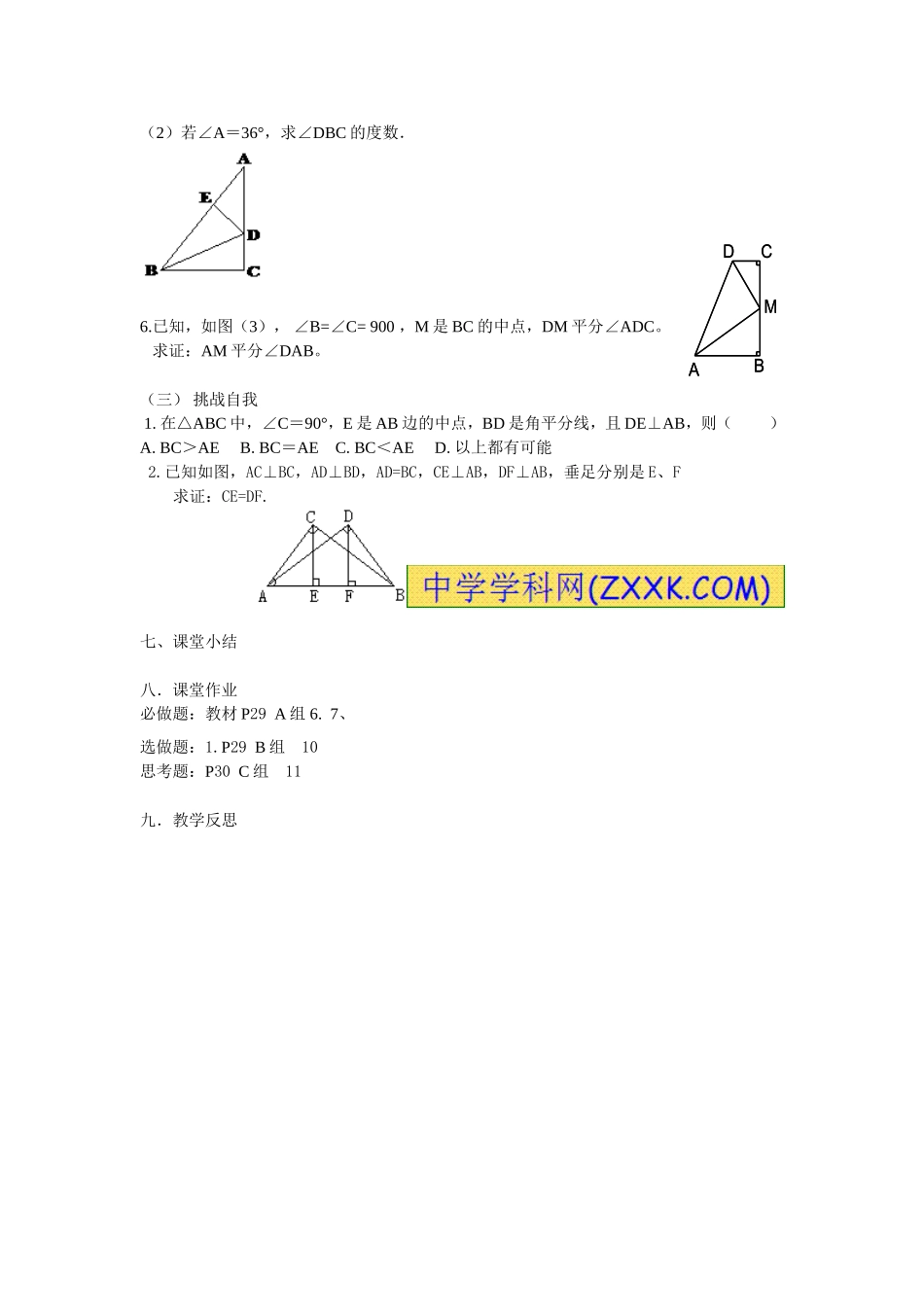
1.5.2直角三角形复习(二)一.学习目标:复习直角三角形全等及角平分线的性质二.教学重点:直角三角形全等及角平分线的性质在证明题中的运用。三.教学方法:自主学习,合作探究,师徒结对,兵教兵四.复习引入(1)判定两个直角三角形全等已经有哪些方法?(2)角平分线有什么性质定理?六、自学检测题:(一)基础检测1、如图,DB⊥AB于点B,DC⊥AC于点C,DB=DC,∠CDA=500,则∠BDA=_______.2、下列条件中不能做出唯一直角三角形的是()A、已知两直角边B、已知两锐角C、已知一直角边和一锐角D、已知斜边和一直角边3.(1)∵OP平分∠AOB,点P在射线OC上,PD⊥OA于D,PE⊥OB于E,∴__________(依据:角平分线上的点到这个角两边的距离相等).(2)∵PD⊥OA,PE⊥OB,PD=PE,∴OP平分∠AOB(依据:___________).(二)一展身手1.如图所示,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=6cm,则△DEB的周长为()A.4cmB.6cmC.10cmD.以上都不对2.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,AE=AC,下列结论中错误的是()A.DC=DEB.∠AED=90°C.∠ADE=∠ADCD.DB=DC3.在Rt△ABC中,∠C=90°,AD是角平分线,若BC=10,BD∶CD=3∶2,则点D到AB的距离是()A.4B.6C.8D.104:已知:如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且BD=CE求证:OB=OC.5.已知:如图,在Rt△ABC中,∠C=90°,D是AC上一点,DE⊥AB于E,且DE=DC.(1)求证:BD平分∠ABC;ACDBACDB(2)若∠A=36°,求∠DBC的度数.6.已知,如图(3),∠B=∠C=900,M是BC的中点,DM平分∠ADC。求证:AM平分∠DAB。(三)挑战自我1.在△ABC中,∠C=90°,E是AB边的中点,BD是角平分线,且DE⊥AB,则()A.BC>AEB.BC=AEC.BC<AED.以上都有可能2.已知如图,AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是E、F求证:CE=DF.七、课堂小结八.课堂作业必做题:教材P29A组6.7、选做题:1.P29B组10思考题:P30C组11九.教学反思AMDCBAMDCB