4.8正弦函数、余弦函数的图象和性质(二)VIP免费

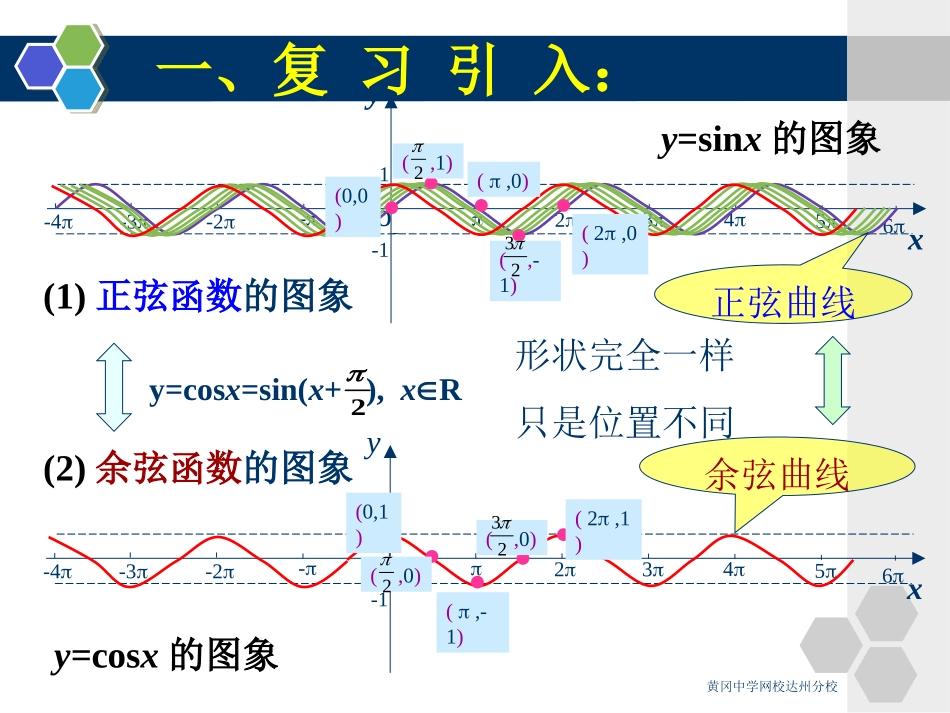
4.8正弦函数、余弦函数的图象和性质（二）2025年1月18日黄冈中学网校达州分校教学目标：1.理解正、余弦函数的定义域、值域。2.会求简单函数的定义域、值域。教学重点：正、余弦函数的定义域、值域教学难点：求复合函数的定义域、值域黄冈中学网校达州分校x6yo--12345-2-3-41(2)余弦函数的图象(1)正弦函数的图象x6yo--12345-2-3-41y=cosx=sin(x+),xR2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同一、复习引入：(0,0)(,1)2(,0)(,-1)23(2,0)y=sinx的图象y=cosx的图象黄冈中学网校达州分校复习：y=sinx和y=cosx的图象黄冈中学网校达州分校正弦函数、余弦函数的图象与性质1.y=sinx和y=cosx的定义域和值域黄冈中学网校达州分校正弦函数、余弦函数的图象和性质f(x)=sinxf(x)=cosx图象定义域值域最值f(x)=0223xy02--1-1223xy02--1-1RR[1,1][1,1])(22Zkkx时ymax=1)(22Zkkx时ymin=1)(2Zkkx时ymax=1)(2Zkkx时ymin=1)(Zkkx)(2Zkkx黄冈中学网校达州分校例1.求下列函数的定义域：(1)sin2yx(1)2xR解：故原函数定义域为R.∴xR，(2)3xR(3)sin0x[2,2]()xkkkZ(2)cos()3yx故原函数定义域为R.∴xR，(3)sinyx故原函数定义域为：[2,2]()kkkZ黄冈中学网校达州分校{|2,}2xRxkkZ2250(5)sin0xx5522()xkxkkZ[5,)[0,)x例1.求下列函数的定义域：1(4)sin1yx2(5)25lgsinyxx(4)sin10x解：sin1x黄冈中学网校达州分校例2.求下列函数的值域：21(1)sin1yxsin(2)sin2xyx2(1)0sin1x解：21sin12x112y1[,1]2所以原函数的值域为2(2)sin1yxy1sin1x又2111yy113y1sin1x所以原函数的值域为1[1,]3黄冈中学网校达州分校(2)当sin2x=-1时,即x=k-4(kZ)时,ymax=3∴函数的最大值为3例3.求下列函数的最大值，并求出最大值时x的集合：(1)y=cos,xR；(2)y=2-sin2x,xR3x解：(1)当cos=1,即x=6k(kZ)时，ymax=13x)(222Zkkx∴函数的最大值为1取最大值时x的集合为{x|x=6k,kZ}．(kZ)}∴取最大值时x的集合为{x|x=k-4黄冈中学网校达州分校例4.求下列函数的定义域和值域(1)xsin11y(2)y=log3(1-2cosx)(3)xsin43y2(4)xcos3xcosy2解答：(1)由题意:1+sinx≠0,∴)Zk(23k2x此时-10得21xcos，又cosx≥-1,∴21xcos1，由图可看出：).Zk(35k2x3k2由21xcos1得0<1-2cosx≤3,∴函数的定义域为}Zk,35k2x3k2|x{.令u=1-2cosx,y=logau, a=3>1,∴y=log3u是增函数，∴log3(1-2cosx)≤1,∴函数的值域是(-∞,1].例4.求下列函数的定义域和值域(2)y=log3(1-2cosx)黄冈中学网校达州分校求定义域时，我们借助了三角函数线，这样可以使问题更直观.当然画三角函数图象观察也可以.而在求值域时，我们利用了复合函数的知识，要注意定义域与它的制约关系.黄冈中学网校达州分校解：(3)由3-4sin2x≥0得43xsin2，∴23xsin23，由43xsin02，∴0≤3-4sin2x≤3.∴函数值域为]30[，.画三角函数线可得：)Zk(3kx3k,∴函数的定义域为：}Zk,3kx3k|x{，例4.求下列函数的定义域和值域(3)xsin43y2黄冈中学网校达州分校解:(4)由题x∈R，即定义域为全体实数.43)23x(cosy2.由x∈R，得-1≤cosx≤1,当cosx=1时，31ymax，评析：此题本质上是二次函数闭区间上的值域问题.其中闭区间就是由cosx决定的.其它几个小题的值域也均是由sinx,cosx的值域决定的.例4.求下列函数的定义域和值域(4)xcos3xcosy2当23xcos时，43ymin，∴函数的值域为]31,43[.黄冈...