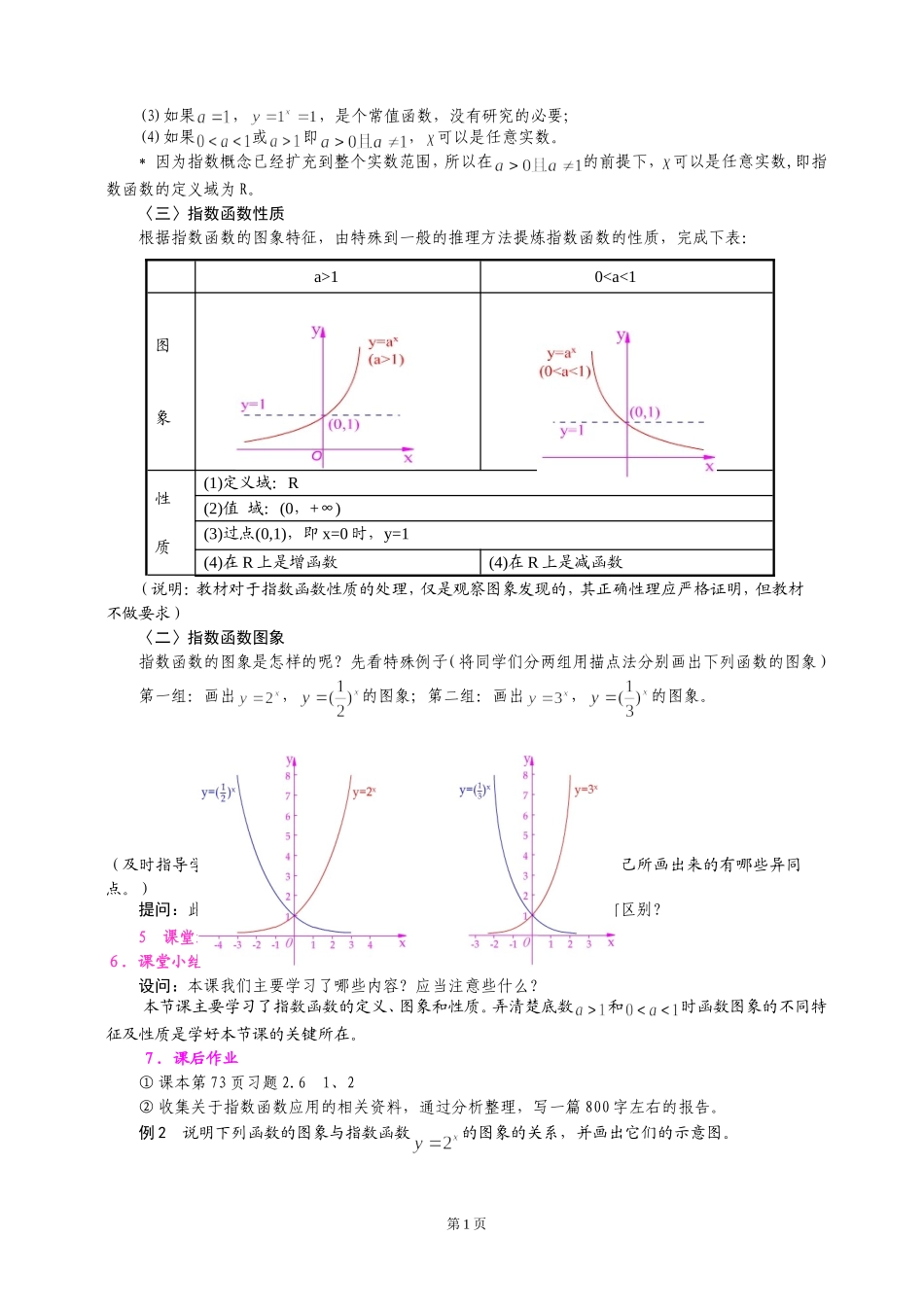
《指数函数》教学设计三、目标分析1.知识技能目标掌握指数函数的概念、图象和性质。2.过程与方法目标通过自主探索,让学生经历“特殊→一般→特殊”的认知过程,完善认知结构,领会数形结合、分类讨论、归纳推理等数学思想方法。3.情感、价值观目标让学生感受数学问题探索的乐趣和成功的喜悦,体会数学的理性、严谨及数与形的和谐统一美,展现数学实用价值及其在社会进步、人类文明发展中的重要作用。二、重难点分析根据新课程标准及对教材的分析,确定本节课重难点如下:重点:本节课是围绕指数函数的概念和图象,并依据图象特征归纳其性质展开的。因此本节课的教学重点是掌握指数函数的图象和性质。难点:1、对于和时函数图象的不同特征,学生不容易归纳认识清楚。因此,弄清楚底数a对函数图象的影响是本节的难点之一。2、底数相同的两个函数图象间的关系。五、教法准备七、教学过程2.新课引入观看视频解答下面两个问题:问题1:某种细胞分裂时,由一个分裂成2个,2个分裂成4个……,这样的细胞分裂x次后,细胞个数y与x的函数关系式为:y=2x(x∈N*)提问:y=2x与y=3x这类函数的解析式有何共同特征?答:函数解析式都是指数形式,底数为定值且自变量在指数位置。(若用a代换两个式子中的底数,并将自变量的取值范围扩展到实数集则得到……)3.探索新知〈一〉指数函数的定义一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。提问:在本定义中要注意哪些要点?1自变量x2定义域R3a的范围a>0,且a≠14定义的形式(对应法则)y=ax进一步提问:为什么规定定义中?将a如数轴所示分为:,,,和五部分进行讨论:(1)如果,比如,这时对于等,在实数范围内函数值不存在;(2)如果,(3)如果,,是个常值函数,没有研究的必要;(4)如果或即,可以是任意实数。*因为指数概念已经扩充到整个实数范围,所以在的前提下,可以是任意实数,即指数函数的定义域为R。〈三〉指数函数性质根据指数函数的图象特征,由特殊到一般的推理方法提炼指数函数的性质,完成下表:a>10