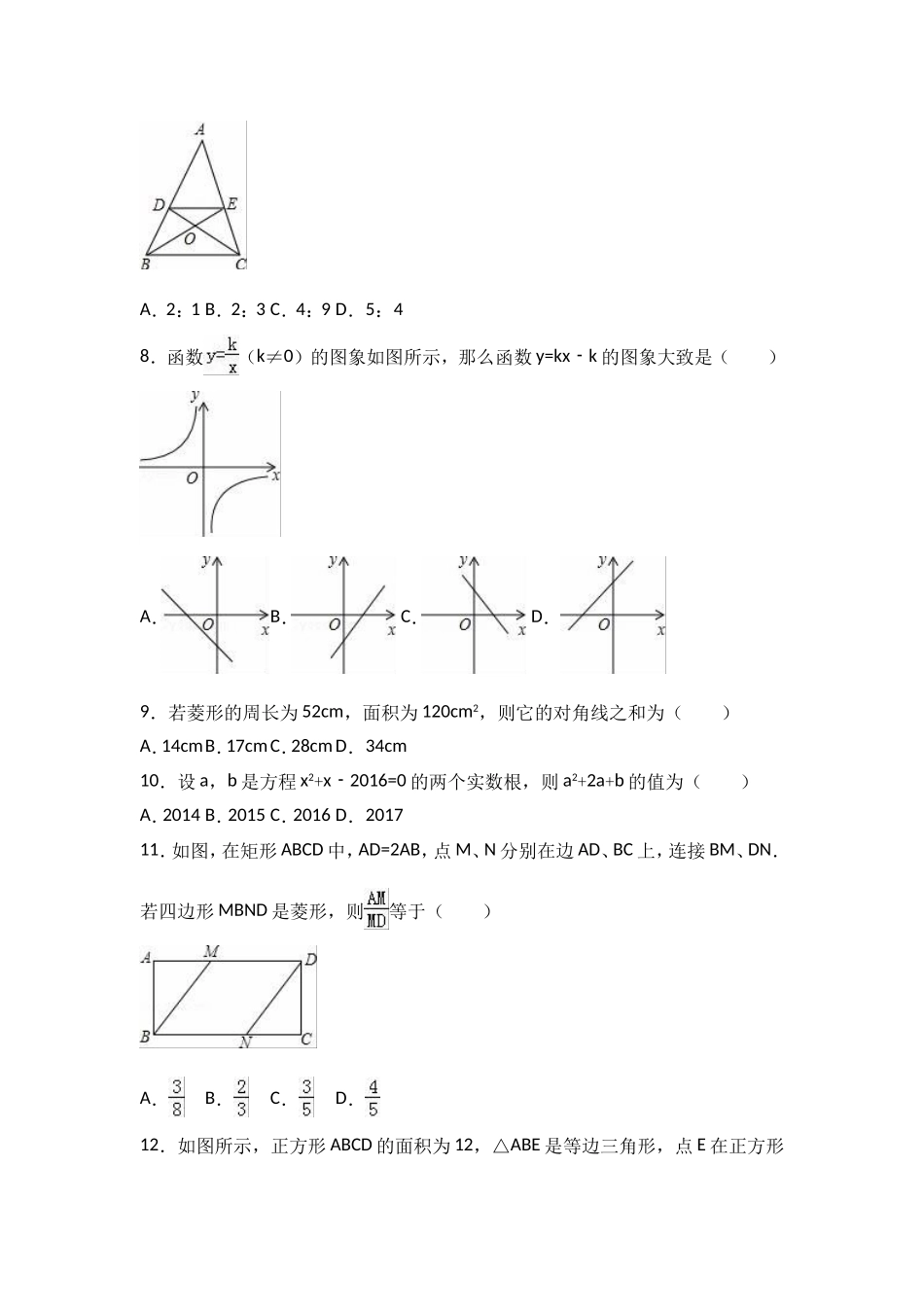
2016-2017学年广东省深圳市南山区九年级(上)期末数学试卷一、选择题(本题有12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确的选项用铅笔涂在答题卡上.)1.若2a=3b,则a:b等于()A.3:2B.2:3C.﹣2:3D.﹣3:22.与如图中的三视图相对应的几何体是()A.B.C.D.3.若关于x的一元二次方程kx22x1=0﹣﹣有两个不相等的实数根,则k的取值范围是()A.k>﹣1B.k>﹣1且k≠0C.k<1D.k<1且k≠04.下列命题中,真命题是()A.两条对角线相等的四边形是矩形B.两条对角线互相垂直的四边形是菱形C.两条对角线互相垂直且相等的四边形是正方形D.两条对角线互相平分的四边形是平行四边形5.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则它的宽约为()A.12.36cmB.13.6cmC.32.36cmD.7.64cm6.已知反比例函数,当x<0时,y随x的增大而增大,则k的值可以是()A.﹣1B.0C.1D.27.如图,已知DE∥BC,CD和BE相交于点O,S△DOE:S△COB=4:9,则AE:EC为()A.2:1B.2:3C.4:9D.5:48.函数(k≠0)的图象如图所示,那么函数y=kxk﹣的图象大致是()A.B.C.D.9.若菱形的周长为52cm,面积为120cm2,则它的对角线之和为()A.14cmB.17cmC.28cmD.34cm10.设a,b是方程x2+x2016=0﹣的两个实数根,则a2+2a+b的值为()A.2014B.2015C.2016D.201711.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A.B.C.D.12.如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为()A.2B.2C.3D.二、填空题:(本题有4小题,每小题3分,共12分.把答案填在答题卡上).13.方程x2=2x的解为.14.某地区为估计该地区黄羊的只数,先捕捉20只黄羊给它们分别作上标志,然后放回,待有标志的黄羊完全混合于黄羊群后,第二次捕捉60只黄羊,发现其中2只有标志.从而估计该地区有黄羊只.15.如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,则线段BF长为cm.16.两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是(把你认为正确结论的序号都填上,答案格式:“①②③④”).三、解答题(本大题有7题,其中17题6分,18题6分,19题7分,20题7分,21题8分,22题8分,23题10分,共52分)17.(6分)解方程(1)x24x5=0﹣﹣(2)5x2+2x1=0﹣.18.(6分)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.19.(7分)阳光下,小亮测量“望月阁”的高AB.(如图),由于观测点与“望月阁”底部间的距离不易测得,因此他首先在直线BM上点C处固定平放一平面镜在镜面上做了一个标记,小亮看着镜面上的标记,他来回走动,走到点D时,看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小亮眼睛与地面的高度ED=1.5米,CD=2米.然后,在阳光下,他们用测影长的方法进行了第二次测量,方法如下:小亮从D点沿DM方向走了16米,到达“望月阁”影子的末端F点处,此时,测得小亮身高FG的影长FH=2.5米,FG=1.65米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“望月阁”的高AB的长度.20.(7分)在“文博会”期间,某公司展销如图所示的长方形工艺品,该工艺...