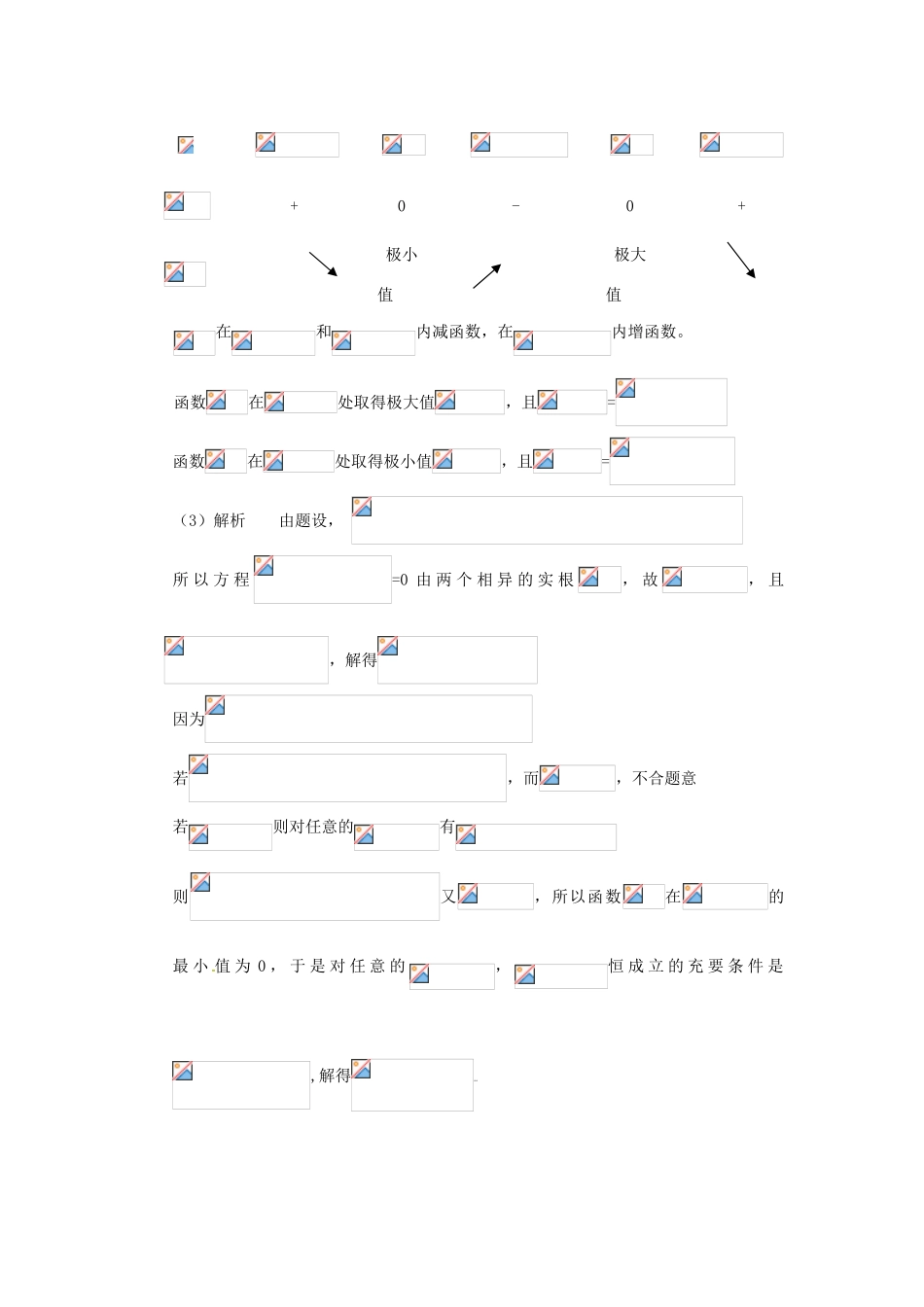
导数训练51(本小题满分12分)设函数.(1)对于任意实数,恒成立,求的最大值;(2)若方程有且仅有一个实根,求的取值范围.解析(1),因为,,即恒成立,所以,得,即的最大值为(2)因为当时,;当时,;当时,;所以当时,取极大值;当时,取极小值;故当或时,方程仅有一个实根.解得或.2.(本小题满分12分)设函数(1)求函数的单调区间;(1)若,求不等式的解集.解析(1),由,得.因为当时,;当时,;当时,;所以的单调增区间是:;单调减区间是:.(2)由,得:.故:当时,解集是:;当时,解集是:;当时,解集是:.3.(本小题满分12分)设函数(Ⅰ)当曲线处的切线斜率(Ⅱ)求函数的单调区间与极值;(Ⅲ)已知函数有三个互不相同的零点0,,且。若对任意的,恒成立,求m的取值范围。答案(1)1(2)在和内减函数,在内增函数。函数在处取得极大值,且=函数在处取得极小值,且=解析解析当所以曲线处的切线斜率为1.(2)解析,令,得到因为当x变化时,的变化情况如下表:+0-0+极小值极大值在和内减函数,在内增函数。函数在处取得极大值,且=函数在处取得极小值,且=(3)解析由题设,所以方程=0由两个相异的实根,故,且,解得因为若,而,不合题意若则对任意的有则又,所以函数在的最小值为0,于是对任意的,恒成立的充要条件是,解得综上,m的取值范围是【考点定位】本小题主要考查导数的几何意义,导数的运算,以及函数与方程的根的关系解不等式等基础知识,考查综合分析问题和解决问题的能力。4.(本小题满分14分)(注意:在试题卷上作答无效)在R上定义运算(b、c为实常数)。记,,.令.如果函数在处有极什,试确定b、c的值;求曲线上斜率为c的切线与该曲线的公共点;记的最大值为.若对任意的b、c恒成立,试示的最大值。解当得对称轴x=b位于区间之外此时由①若于是①若,则,于是综上,对任意的b、c都有而当,时,在区间上的最大值故对任意的b,c恒成立的k的最大值为5(本小题满分12分)已知函数的图象在与轴交点处的切线方程是。(I)求函数的解析式;(II)设函数,若的极值存在,求实数的取值范围以及函数取得极值时对应的自变量的值.解析(I)由已知,切点为(2,0),故有,即……①又,由已知得……②联立①②,解得.所以函数的解析式为…………………………………4分(II)因为令当函数有极值时,则,方程有实数解,由,得.①当时,有实数,在左右两侧均有,故函数无极值②当时,有两个实数根情况如下表:+0-0+↗极大值↘极小值↗所以在时,函数有极值;当时,有极大值;当时,有极小值;…………………………………12分