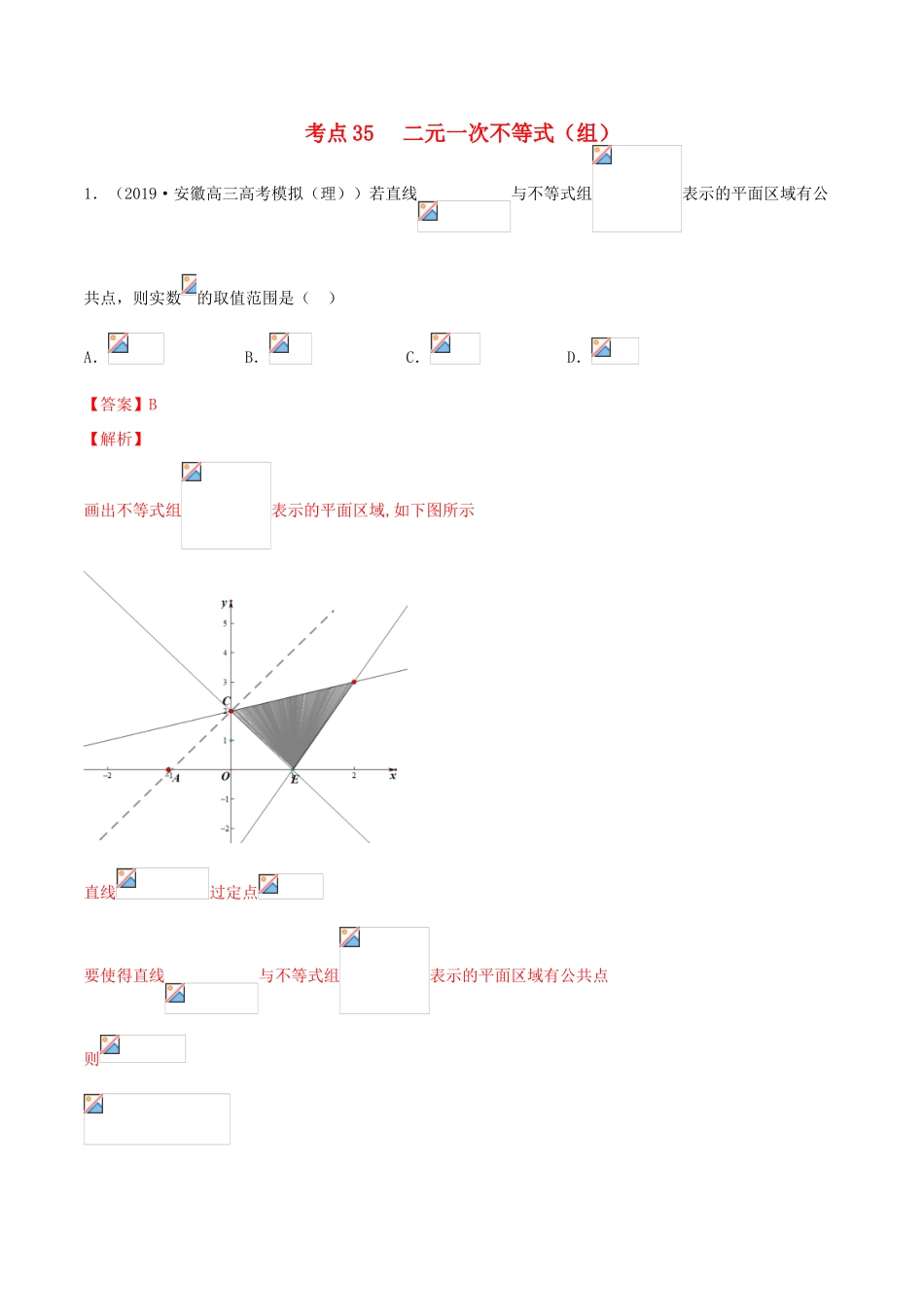
考点35二元一次不等式(组)1.(2019·安徽高三高考模拟(理))若直线与不等式组表示的平面区域有公共点,则实数的取值范围是()A.B.C.D.【答案】B【解析】画出不等式组表示的平面区域,如下图所示直线过定点要使得直线与不等式组表示的平面区域有公共点则.故选B2.(2019·湖南长沙一中高三高考模拟(理))已如定点P,动点Q在线性约束条件所表示的平面区域内,则直线PQ的斜率k的取值范围为()A.B.C.D.【答案】C【解析】不等式组表示的平面区域是如图所示阴影部分,直线与直线的交点为,直线与轴的交点为,只需求出过p的直线经过可行域内的点A或B时的斜率,,,所以结合图象可得或,故选C.3.(2019·福建高三高考模拟(理))已知平面区域:,:,则点是的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】B【解析】平面区域,表示圆以及内部部分;的可行域如图三角形区域:则点P(x,y)∈Ω1是P(x,y)∈Ω2的必要不充分条件.故选:B.4.(2018·湖南长沙一中高三高考模拟(理))在平面直角坐标系中,为不等式组所表示的区域上一动点,则的最小值是()A.1B.C.2D.【答案】B【解析】作出不等式组表示的可行域如图中阴影部分所示,过点O向直线作垂线,垂足在可行域内,所以O到直线的距离即为的最小值,所以.故选B.5.(2019·福建高三高考模拟(理))已知,,,平面区域是由所有满足的点组成的区域,则区域的面积是().A.8B.12C.16D.20【答案】C【解析】由,,,得,,因为所以,解得又因为代入化简得画出不等式组代表的平面区域如图中阴影部分,且阴影部分为平行四边形由直线方程解出点,,,点到直线的距离,所以阴影部分面积为故选:C.6.(2019·北京高三高考模拟(理))设不等式组所表示的平面区域为,其面积为.①若,则的值唯一;②若,则的值有2个;③若为三角形,则;④若为五边形,则.以上命题中,真命题的个数是()A.B.C.D.【答案】C【解析】由题得不等式|x|+|y|≤2,表示的是如图所示的正方形区域,不等式y+2≤k(x+1),表示的是经过定点(-1,-2)的动直线y+2=k(x+1)的一侧(与k的正负有关),所以不等式组所表示的平面区域就是它们的公共部分,(1)因为大正方形的面积为8,若,面积为正方形面积的一半,且过原点O的任意直线均可把正方形的面积等分,故当S=4时,直线必过原点,所以k=2,k的值唯一,命题正确;(2)左边阴影三角形的面积为1,故当k取适当的负值左倾可以使三角形的面积为,k取适当的正值,使得阴影部分的面积为,故S=时,k的值有两个,故该命题正确;(3)由(2)的讨论可知,当k<-2时,左边也有一个三角形,所以当D为三角形时,k的取值范围为,故该命题错误;(4)经过点(-1,-2)和(0,2)的直线绕定点(-1,-2)向左旋转一点,D就是五边形,此时k>.故命题正确.故选:C7.(2019·北京高三高考模拟(理))记不等式组所表示的平面区域为.“点”是“”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】C【解析】画出可行域和点如下图所示,将旋转到点的位置,得,当时,;当时,.故“点”是“”的充分必要条件.故选C.8.(2019·江西高三高考模拟(理))已知,给出下列四个命题::,;:,;:,;:,;其中真命题是()A.和B.和C.和D.和【答案】B【解析】不等式组的可行域如图,当z=x+y过A(﹣2,0)点时,z最小,可得:﹣2+0=﹣2,当z=x+y过B或C点时,z最大,可得:z=2,故P1:,为真命题;P3:,为假命题;又表示可行域内的点与(-3,0)连线的斜率,∴由A(﹣2,0)点,可得0,故P2:∀(x,y)∈D,0错误;由(﹣1,1)点,x2+y2=2故p4:∃(x,y)∈D,x2+y2≤2为真命题.可得选项和正确.故选:B.9.(2019·江西新余一中高三高考模拟(理))已知实数,满足线性约束条件,则其表示的平面区域外接圆的面积为().A.B.C.D.【答案】C【解析】由线性约束条件,画出可行域如图(及内部,又与y=x垂直,∴为直角,即三角形ABC为直角三角形,∴外接圆的直径为AC,又A(-1,3),C(-1,-1),AC=4,∴外接圆的半径r=2,∴外接...