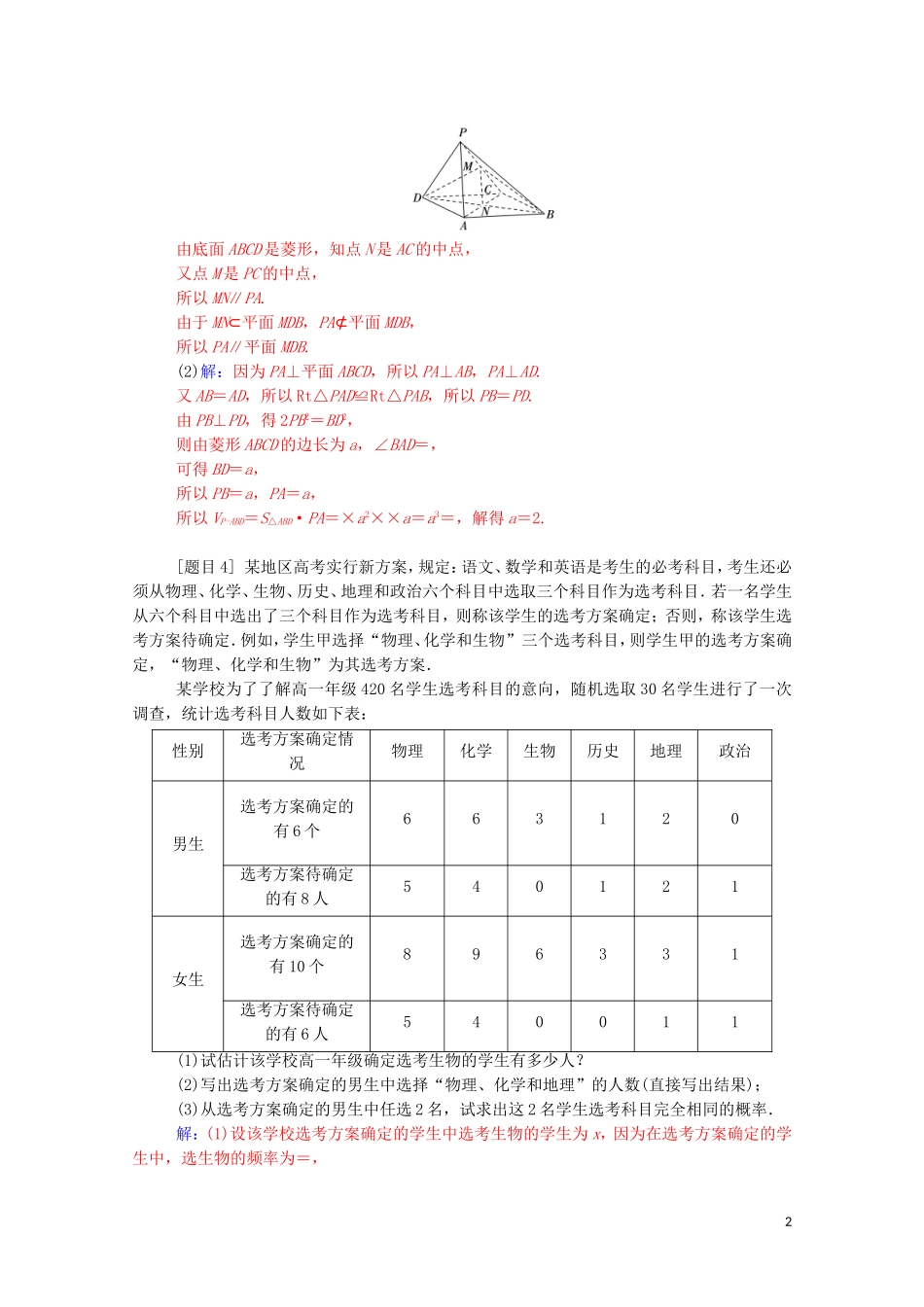
每日一题规范练(第三周)[题目1]在锐角△ABC中,角A,B,C所对的边分别为a,b,c.已知cos2C=-.(1)求sinC;(2)当c=2a,且b=3时,求a.解:(1)因为cos2C=-,即1-2sin2C=-.又0<C<,所以sinC==.(2)由(1)知sinC=,且△ABC是锐角三角形,所以cosC==.因为c=2a,=,所以sinA=sinC=,cosA=.所以sinB=sin[π-(A+C)]=sin(A+C)=sinAcosC+cosAsinC=.因为=,b=3,所以a=2.[题目2]已知等比数列{an}的前n项和为Sn,公比q>1,且a2+1为a1,a3的等差中项,S3=14.(1)求数列{an}的通项公式;(2)记bn=an·log2an,求数列{bn}的前n项和Tn.解:(1)由题意,得2(a2+1)=a1+a3.又S3=a1+a2+a3=14,所以2(a2+1)=14-a2,所以a2=4.因为S3=+4+4q=14,所以q=2或q=.又q>1,所以公比q=2.因此an=a2qn-2=4·2n-2=2n.(2)由(1)知an=2n,所以bn=an·log2an=n·2n,所以Tn=1×21+2×22+3×23+…+(n-1)×2n-1+n×2n.所以2Tn=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1.两式相减得-Tn=2+22+23+24+…+2n-n×2n+1=-n×2n+1=(1-n)2n+1-2.故Tn=(n-1)2n+1+2.[题目3]如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且∠BAD=,点M是PC的中点.(1)求证:PA∥平面MDB;(2)设菱形ABCD的边长为a,若PB⊥PD,三棱锥PABD的体积为,求实数a的值.(1)证明:连接AC,与BD交于点N,连接MN(如图),1由底面ABCD是菱形,知点N是AC的中点,又点M是PC的中点,所以MN∥PA.由于MN⊂平面MDB,PA⊄平面MDB,所以PA∥平面MDB.(2)解:因为PA⊥平面ABCD,所以PA⊥AB,PA⊥AD.又AB=AD,所以Rt△PAD≌Rt△PAB,所以PB=PD.由PB⊥PD,得2PB2=BD2,则由菱形ABCD的边长为a,∠BAD=,可得BD=a,所以PB=a,PA=a,所以VP-ABD=S△ABD·PA=×a2××a=a3=,解得a=2.[题目4]某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还必须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:性别选考方案确定情况物理化学生物历史地理政治男生选考方案确定的有6个663120选考方案待确定的有8人540121女生选考方案确定的有10个896331选考方案待确定的有6人540011(1)试估计该学校高一年级确定选考生物的学生有多少人?(2)写出选考方案确定的男生中选择“物理、化学和地理”的人数(直接写出结果);(3)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.解:(1)设该学校选考方案确定的学生中选考生物的学生为x,因为在选考方案确定的学生中,选生物的频率为=,2所以估计选择“生物”的概率约为.所以选择生物的人数约为x=420×=126(人).(2)由统计图表知,选考方案确定的男生中选择“物理、化学和地理”的人数有2人.(3)设选择物理、生物、化学的学生分别为A1,A2,A3,选择物理、化学、历史的学生为B1,选择物理、化学、地理的学生分别为C1,C2,所以任取2名男生的基本事件有(A1,A2),(A2,A3),(A3,B1),(B1,C1),(C1,C2),(A1,A3),(A2,B1),(A3,C1),(B1,C2),(A1,B1),(A2,C1),(A3,C2),(A1,C1),(A2,C2),(A1,C2)共15种结果.所以,两名男生选考科目完全相同的基本事件共有4个,分别为(A1,A2),(A2,A3),(C1,C2),(A1,A3).所以,2名学生选考科目完全相同的概率为.[题目5]已知椭圆+=1(a>b>0)上的点到右焦点F(c,0)的最大距离是+1,且1,a,4c成等比数列.(1)求椭圆的方程;(2)过点F且与x轴不垂直的直线l与椭圆交于A,B两点,线段AB的中垂线交x轴于点M(m,0)求实数m的取值范围.解:(1)由于1,a,4c成等比数列,所以1×4c=2a2,即a2=2c.①又a+c=+1.②联立①②得a=,c=1.则b2=a2-c2=1.所以椭圆的方程为+y2=...