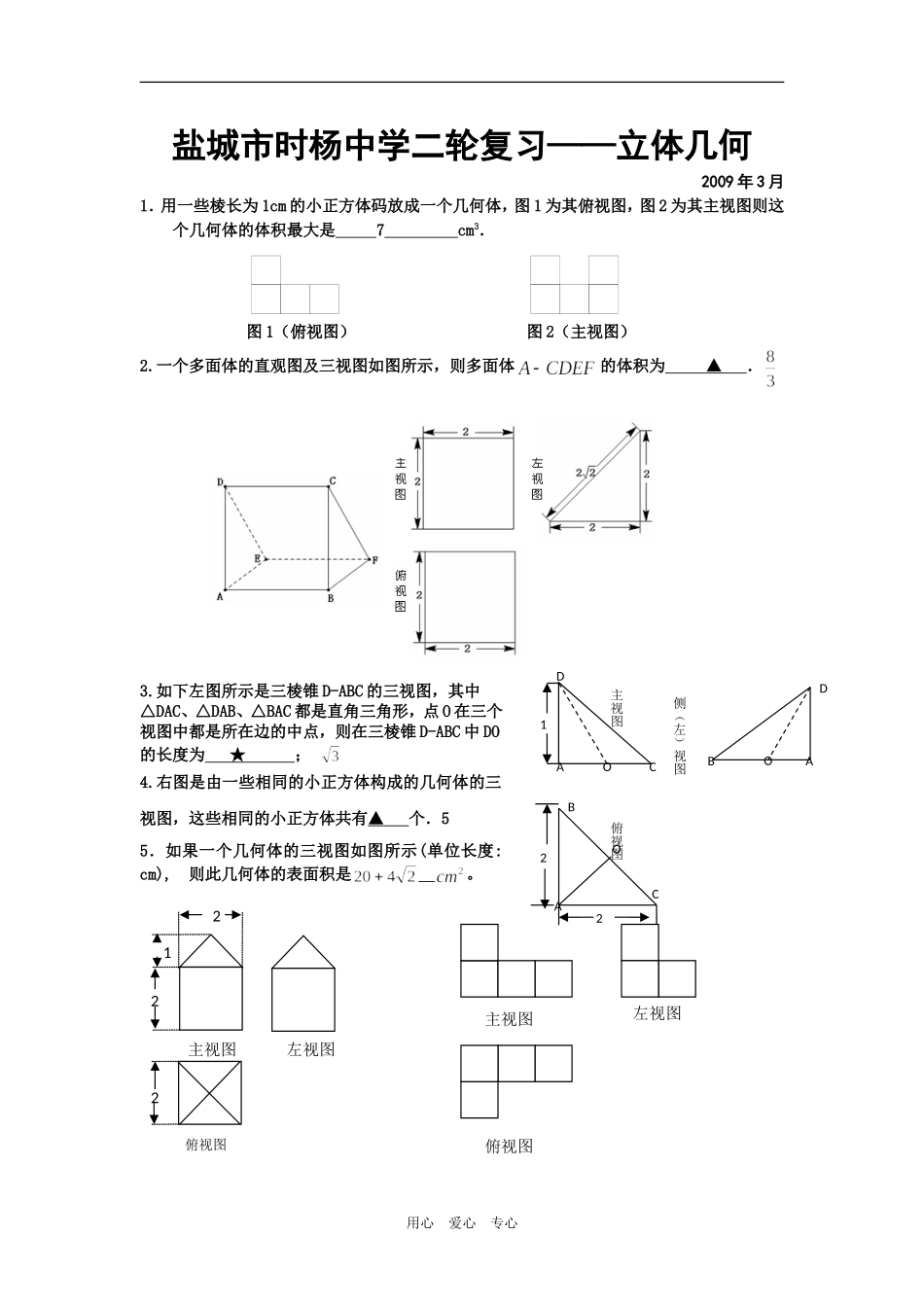
盐城市时杨中学二轮复习——立体几何2009年3月1.用一些棱长为1cm的小正方体码放成一个几何体,图1为其俯视图,图2为其主视图则这个几何体的体积最大是7cm3.图1(俯视图)图2(主视图)2.一个多面体的直观图及三视图如图所示,则多面体的体积为▲.3.如下左图所示是三棱锥D-ABC的三视图,其中△DAC、△DAB、△BAC都是直角三角形,点O在三个视图中都是所在边的中点,则在三棱锥D-ABC中DO的长度为★;4.右图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体共有▲个.55.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是。用心爱心专心DADABCOOBACO122主视图侧(左)视图俯视图主视图俯视图左视图2俯视图主视图左视图2126.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为7.一个几何体的三视图中,正视图和侧视图都是矩形,俯视图是等腰直角三角形(如图),根据图中标注的长度,可以计算出该几何体的表面积是12+4.8.已知:正方体,,E为棱的中点.⑴求证:;⑵求证:平面;⑶求三棱锥的体积证明:连结,则//, 是正方形,∴. 面,∴.又,∴面. 面,∴,∴.⑵证明:作的中点F,连结. 是的中点,∴,∴四边形是平行四边形,∴. 是的中点,∴,又,∴.∴四边形是平行四边形,//, ,,∴平面面.又平面,∴面9.如图,在三棱柱中,四边形为菱形,,四边形为矩形,若且,⑴求证:平面平面;⑵求三棱柱的体积.⑴略;⑵.10.一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点).(I)求证:MN∥平面CDEF;(II)求多面体A—CDEF的体积.用心爱心专心C1B1CBA1AC1B1A1CBA解:由三视图可知,该多面体是底面为直角三角形的直三棱住ADE—BCF,且AB=BC=BF=2,DE=CF=2∴∠CBF=(1)取BF中点G,连MG、NG,由M、N分别为AF、BC的中点可得,NG∥CF,MG∥EF,∴平面MNG∥平面CDEF.∴MN∥平面CDEF.(2)取DE的中点H. AD=AE,∴AH⊥DE,在直三棱柱ADE—BCF中,平面ADE⊥平面CDEF,面ADE∩面CDEF=DE.∴AH⊥平面CDEF.∴多面体A—CDEF是以AH为高,以矩形CDEF为底面的棱锥,在△ADE中,AH=,∴棱锥A—CDEF的体积为11.多面体中,,,,。(1)求证:;(2)求证:。证明:(1) ∴(2)令中点为,中点为,连结、 是的中位线∴又 ∴∴∴ 为正∴∴又 ,∴四边形为平行四边形∴∴用心爱心专心ABCDEMNABCDE12.在斜三棱柱A1B1C1-ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.(Ⅰ)若D是BC的中点,求证:AD⊥CC1;(Ⅱ)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;16、(Ⅰ) AB=AC,D是BC的中点,∴AD⊥BC. 底面ABC⊥平面BB1C1C,面ABC面∴AD⊥侧面BB1C1C.------4面∴AD⊥CC1.------6(Ⅱ)延长B1A1与BM交于N,连结C1N. AM=MA1,∴NA1=A1B1. A1B1=A1C1,∴A1C1=A1N=A1B1.∴C1N⊥C1B1.------9 截面NB1C1⊥侧面BB1C1C,面NB1C1面BB1C1C=C1B1∴C1N⊥侧面BB1C1C.面C1NB------12∴截面C1NB⊥侧面BB1C1C.∴截面MBC1⊥侧面BB1C1C.------1415.直三棱柱中,,.(1)求证:平面平面;(2)求三棱锥的体积.解:(1)直三棱柱ABC—A1B1C1中,BB1⊥底面ABC,则BB1⊥AB,BB1⊥BC,又由于AC=BC=BB1=1,AB1=,则AB=,则由AC2+BC2=AB2可知,AC⊥BC,又由上BB1⊥底面ABC可知BB1⊥AC,则AC⊥平面B1CB,所以有平面AB1C⊥平面B1CB;(2)三棱锥A1—AB1C的体积.(注:还有其它转换方法)13.如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,M,N分别为A1B,B1C1的中点.(1)求证BC∥平面MNB1;(2)求证平面A1CB⊥平面ACC1A1.用心爱心专心ABCDA1B1C1MABCC1A1B1ABCMNA1B1C1(第16题)证明:(1)因BC∥B1C1,且B1C1平面MNB1,BC平面MNB1,故BC∥平面MNB1.(2)因BC⊥AC,且ABC-A1B1C1为直三棱柱,故BC⊥平面ACC1A1.因BC平面A1CB,故平面A1CB⊥平面ACC1A1.14.如图,在四棱锥中,平面平面,,是等边三角形,已知,.(Ⅰ)设是上的一点,证明:平面平面;(Ⅱ)求四棱锥的体积.解:(Ⅰ)证明:在中,由于,,,所以.故.又平面平面,平面平面,平面,所以平面,又平面,故平面平面....