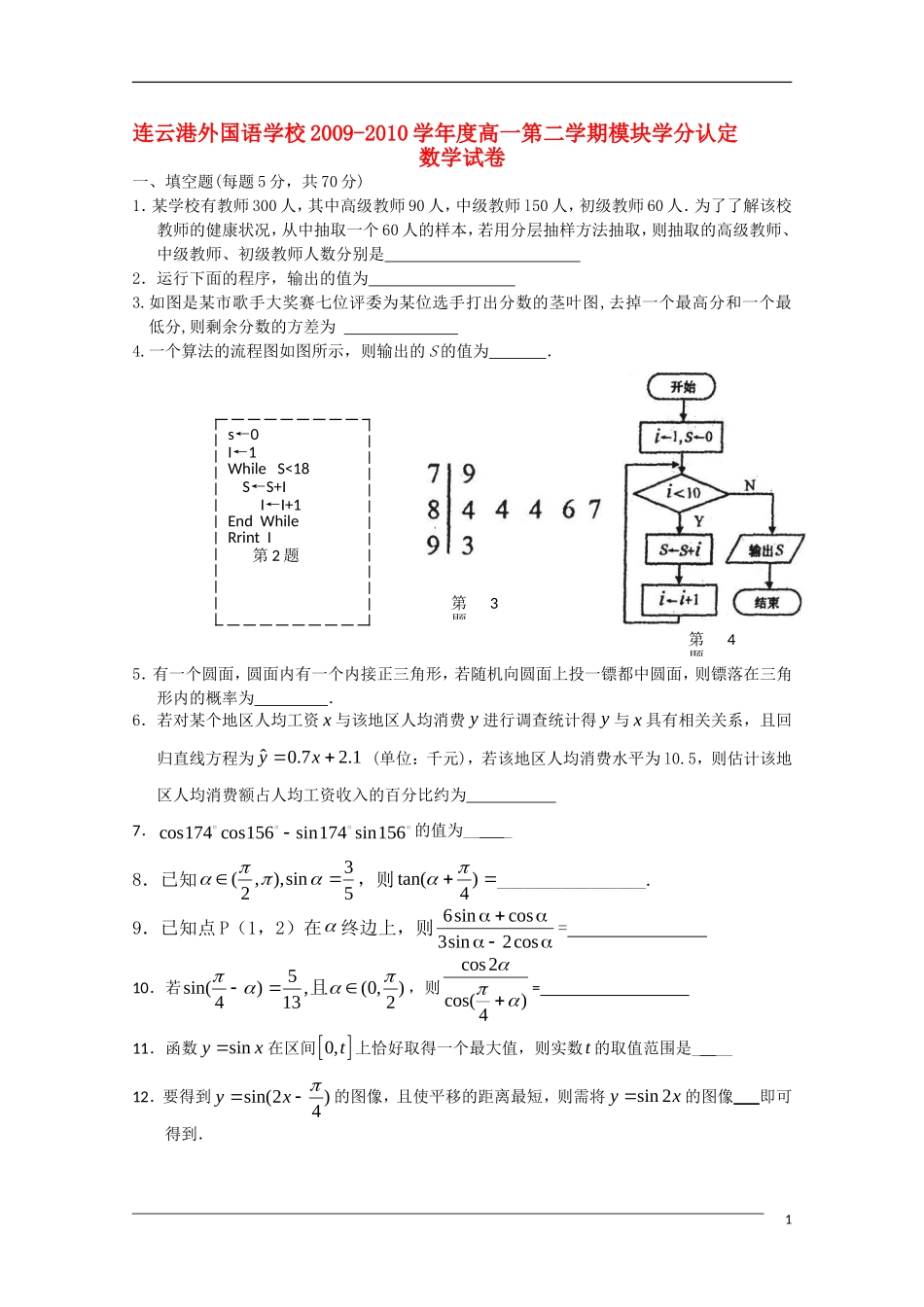
连云港外国语学校2009-2010学年度高一第二学期模块学分认定数学试卷一、填空题(每题5分,共70分)1.某学校有教师300人,其中高级教师90人,中级教师l50人,初级教师60人.为了了解该校教师的健康状况,从中抽取一个60人的样本,若用分层抽样方法抽取,则抽取的高级教师、中级教师、初级教师人数分别是2.运行下面的程序,输出的值为3.如图是某市歌手大奖赛七位评委为某位选手打出分数的茎叶图,去掉一个最高分和一个最低分,则剩余分数的方差为4.一个算法的流程图如图所示,则输出的S的值为.5.有一个圆面,圆面内有一个内接正三角形,若随机向圆面上投一镖都中圆面,则镖落在三角形内的概率为.6.若对某个地区人均工资x与该地区人均消费y进行调查统计得y与x具有相关关系,且回归直线方程为1.27.0ˆxy(单位:千元),若该地区人均消费水平为l0.5,则估计该地区人均消费额占人均工资收入的百分比约为7.cos174cos156sin174sin156的值为___8.已知53sin),,2(,则)4tan(________________.9.已知点P(1,2)在终边上,则cos2sin3cossin6=10.若)2,0(,135)4sin(且,则)4cos(2cos=11.函数sinyx在区间0,t上恰好取得一个最大值,则实数t的取值范围是___12.要得到)42sin(xy的图像,且使平移的距离最短,则需将sin2yx的图像即可得到.1s←0I←1WhileS<18S←S+II←I+1EndWhileRrintI第2题第3题第4题13.在△ABC中,AC=2B,则2tan2tan32tan2tanCACA14.若正方形ABCD边长为1,点P在线段AC上运动,则)(PDPBAP的取值范围是二、解答题(6大题,共90分)15.据统计,从5月1日到5月7号参观上海世博会的人数如下表所示:日期1日2日3日4日5日6日7日人数(万)2123131591214其中,5月1日到5月3日为指定参观日,5月4日到5月7日为非指定参观日.(Ⅰ)把这7天的参观人数看成一个总体,求该总体的平均数(精确到0.1)(Ⅱ)用简单随机抽样方法从非指定参观日中抽取2天,它们的参观人数组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过2万的概率(本题14分)16.从某校参加高一年级基础知识数学测试的450名同学中,随机抽取若干名同学,将他们的成绩制成如下频率分布表.(1)根据表中已知数据,填写在①、②、③处的数值分别为,,;(2)补全在区间[90,160]上的频率分布直方图;(3)请你估计该校成绩不低于130分的同学人数.(本题14分)17.(本题14分)在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱。2分组频数频率[90,100)0.08[100,110)②[110,120)0.36[120,130)160.32[130,140)0.O8[140,150)2①[150,160]0.O2合计③(1)摸出的3个球为白球的概率是多少?(2)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一天能赚多少钱?18.已知,,ABC是ABC的三个内角,向量(1),m�,3(cos,sin)nAA,且1mn�(I)求角A;(Ⅱ)若3sincos2sin122BBB,求tanC.(本题16分)19.已知函数Rxxxxxxf,cos3cossin2sin)(22(1)写出函数)(xf的最小正周期和单调递增区间;(2)若511)2(xf且x0,求xtan的值.(本题16分)320.已知向量4cos,sin,cos,sin,cos,sin5cosOMONxxPQxx�(1)当4cos5sinx时,求函数yONPQ�的最小正周期(2)当12,13OMONOM�∥,,PQxx�都是锐角时,求cos2的值.(本题16分)连云港外国语学校2009-2010学年度第二学期模块学分认定数学答题纸一、填空题(每题5分,共70分)1、8、2、9、3、10、4班级姓名学号考试号班级\(1)填写在处的数值分别为,,;(2)补全在区间[90,160]上的频率分布直方图.(3)解答如下:4、11、5、12、6、13、7、14、二、解答题(共90分)15、(共14分)16(共14分)517、(共14分)18、(共16分)19、(共16分)62...