高考数学复习点拨 3.1~3.2教材解读VIP免费

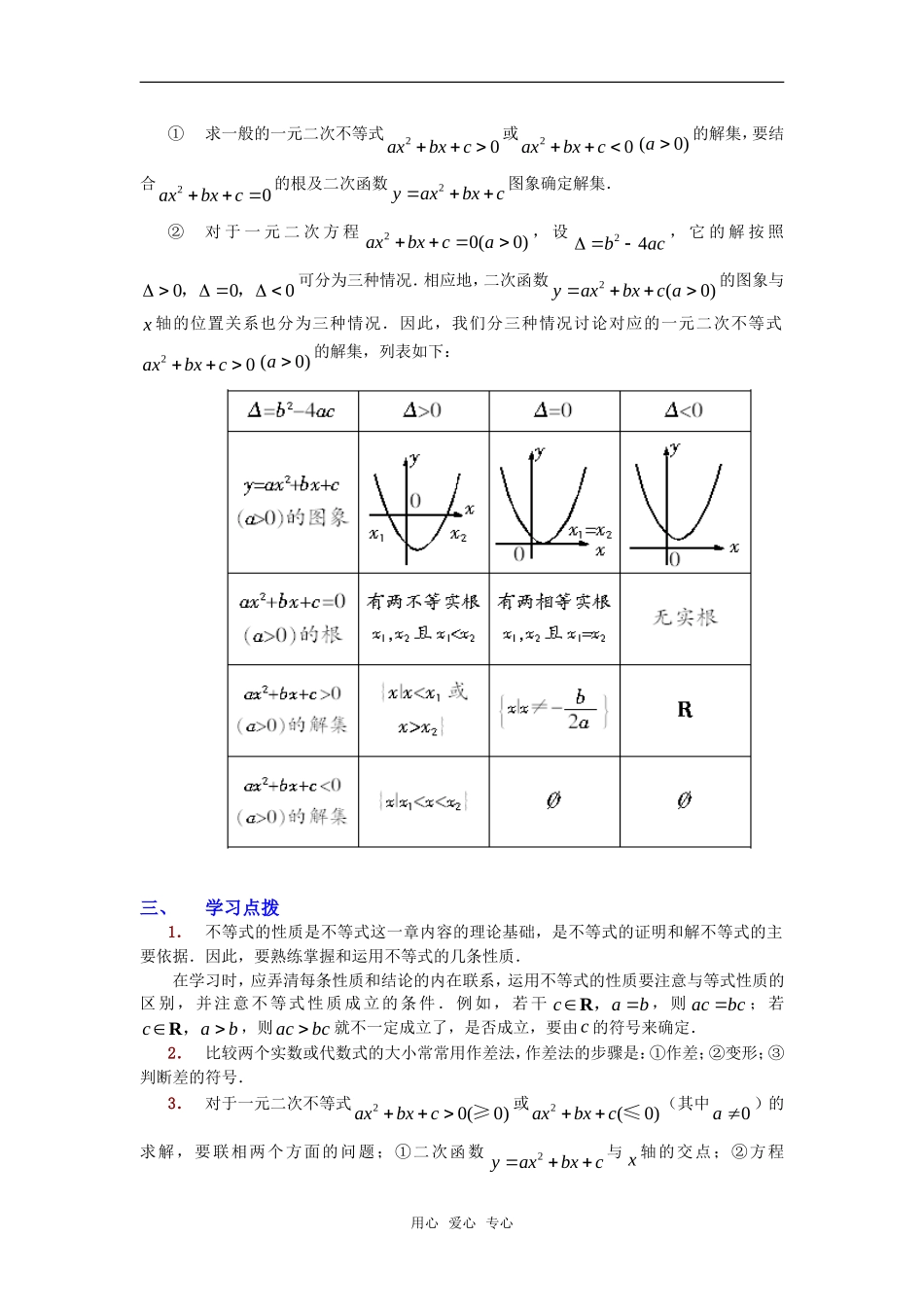
高中数学.1~3.2教材解读一、学习目标1．不等式与不等关系：理解不等式与不等关系的概念，并能了解一些不等式的性质和不等式的意义；体验现实生活中一些不等关系，会比较两个实数及两个代数式的大小，并学习一些简单的不等式证明的有关知识．2．一元二次不等式及其解法：经历从实际情景中抽象出一元二次不等式模型的过程；掌握一元二次不等式的解法，并通过函数图像了解一元二次不等式与一元二次方程以及一元二次函数之间的内在联系，尝试设计求解的程序框图．二、知识精讲1．不等关系与不等式（1）不等式的定义用不等号（＜，＞，≤，≥，）表示不等关系的式子叫做不等式．记作()()fxgx，()()fxgx≥等等．（2）不等式的分类①绝对值不等式；②条件不等式；③矛盾不等式．（3）关于ab≤中ab≥的含义不等式ab≤应读作“a小于或者等于b”，其含义是指“或者ab，或者ab”，即ab或ab之中有一个正确，则ab≤正确．不等式ab≥应读作“a大于或者等于b”，其含义是指“ab，或者ab”，即ab或ab之中有一个正确，则ab≥正确．（4）不等式的基本性质①abbcac，②00abcacbcabcacbc，；，③abacbc④abcdacbd，⑤00abcdacbd，⑥01nnnnabnnababN，，；（5）实数比较大小的理论①对于任意两个实数()ababR，，000abababababab；；．②设abR，，则1aabb；1aabb；1aabb．2．一元二次不等式及其解法（1）一元二次不等式我们把只含有一个未知数，并且未知数的最高次数是2的不等式叫做一元二次不等式．（2）一元二次不等式与相应的函数，方程的联系用心爱心专心①求一般的一元二次不等式20axbxc或20axbxc(0)a的解集，要结合20axbxc的根及二次函数2yaxbxc图象确定解集．②对于一元二次方程20(0)axbxca，设24bac，它的解按照000，，可分为三种情况．相应地，二次函数2(0)yaxbxca的图象与x轴的位置关系也分为三种情况．因此，我们分三种情况讨论对应的一元二次不等式20axbxc(0)a的解集，列表如下：三、学习点拨1．不等式的性质是不等式这一章内容的理论基础，是不等式的证明和解不等式的主要依据．因此，要熟练掌握和运用不等式的几条性质．在学习时，应弄清每条性质和结论的内在联系，运用不等式的性质要注意与等式性质的区别，并注意不等式性质成立的条件．例如，若干cabR，，则acbc；若cabR，，则acbc就不一定成立了，是否成立，要由c的符号来确定．2．比较两个实数或代数式的大小常常用作差法，作差法的步骤是：①作差；②变形；③判断差的符号．3．对于一元二次不等式20(0)axbxc≥或2(0)axbxc≤（其中0a）的求解，要联相两个方面的问题；①二次函数2yaxbxc与x轴的交点；②方程用心爱心专心20axbxc的根．因此，解一元二次不等式的过程，体现了函数与方程、数形结合等数学思想方法的运用．4．用一元二次不等式解决实际问题的操作步骤是：（1）理解题意，搞清量与量之间的关系；（2）建立相应的不等式关系，把实际问题抽象为数学中的一元二次不等式问题；（3）解这个一元二次不等式，得到实际问题的解．用心爱心专心