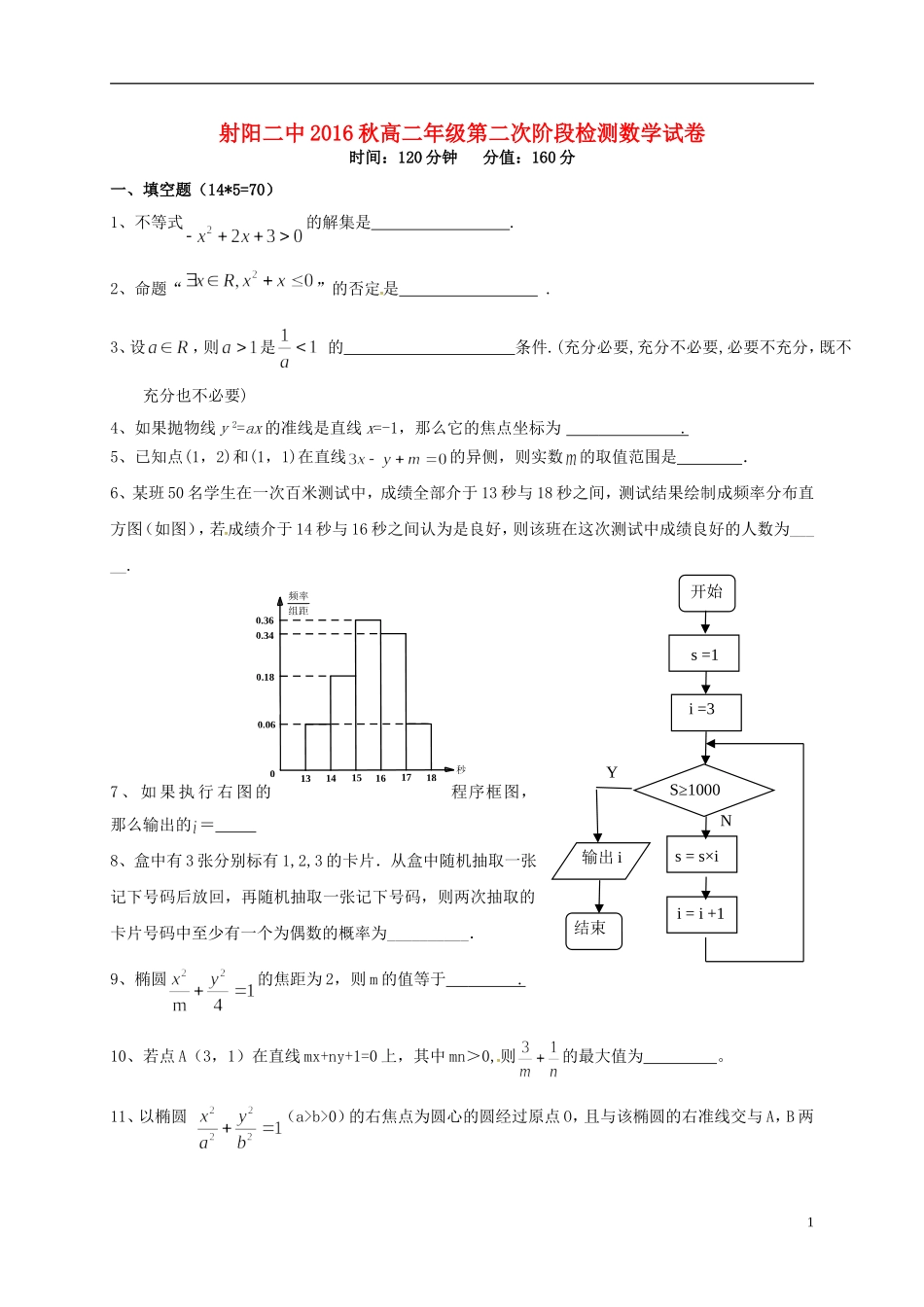
频率组距秒18171615141300.060.180.340.36射阳二中2016秋高二年级第二次阶段检测数学试卷时间:120分钟分值:160分一、填空题(14*5=70)1、不等式的解集是.2、命题“”的否定是.3、设,则是的条件.(充分必要,充分不必要,必要不充分,既不充分也不必要)4、如果抛物线y2=ax的准线是直线x=-1,那么它的焦点坐标为.5、已知点(1,2)和(1,1)在直线的异侧,则实数的取值范围是.6、某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,测试结果绘制成频率分布直方图(如图),若成绩介于14秒与16秒之间认为是良好,则该班在这次测试中成绩良好的人数为_____.7、如果执行右图的程序框图,那么输出的=8、盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为__________.9、椭圆的焦距为2,则m的值等于.10、若点A(3,1)在直线mx+ny+1=0上,其中mn>0,则的最大值为。11、以椭圆(a>b>0)的右焦点为圆心的圆经过原点O,且与该椭圆的右准线交与A,B两1开始s=1i=3S≥1000s=s×ii=i+1输出i结束NY点,已知△OAB是正三角形,则该椭圆的离心率是12、平面直角坐标系xoy中,抛物线的焦点为F,设M是抛物线上的动点,则的最大值是13、若关于的不等式至少有一个负数解,则实数的取值范围是.14、设椭圆C的左右焦点分别为是右准线,若椭圆上存在一点P使得是P到直线l的距离的3倍,则椭圆的离心率的取值范围是.二、解答题(14+14+15+15+16+16)15.已知:方程有两个不相等的实数根;:不等式的解集为.若“”为真,“”为假,求实数的取值范围.16、(1)已知椭圆的离心率为,准线方程为,求该椭圆的标准方程(2)求与双曲线x2-2y2=2有公共渐近线,且过点M(2,-2)的双曲线方程.217、某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年的蔬菜销售收入均为50万元,设表示前年的纯利润总和(=前年的总收入前年的总支出投资额).(1)该厂从第几年开始盈利?(2)若干年后,投资商为开发新项目,对该厂有两种处理方案:①当年平均利润达到最大时,以48万元出售该厂;②当纯利润总和达到最大时,以16万元出售该厂,问哪种方案更合算?18.如图)0,(),0,(21cFcF为双曲线E的两焦点,以12FF为直径的圆O与双曲线E交于11,,,,MNMNB是圆O与y轴的交点,连接1MM与OB交于H,且H是OB的中点,(1)当1c时,求双曲线E的方程;(2)试证:对任意的正实数c,双曲线E的离心率为常数.319、已知函数,的解集为(-3,2),(1)求的解析式;(2)时,的最大值;(3)若不等式的解集为A,且,求实数的取值范围.20、设椭圆方程+=1(a>b>0),椭圆上一点到两焦点的距离和为4,过焦点且垂直于x轴的直线交椭圆于A,B两点,AB=2.(1)求椭圆方程;(2)若M,N是椭圆C上的点,且直线OM与ON的斜率之积为﹣,是否存在动点P(x0,y0),若=+2,有x02+2y02为定值.4射阳二中2016秋高二年级第二次阶段检测数学试卷答案命题人:崔常娥时间:120分钟分值:160分1、(-1,3)2、3、充分不必要条件4、(1,0)5、(-2,-1)6、277、88、9、5或310、-l611、12、13、14、15、解:p为真:2m,q为真:当p真q假:当p假q真:综上:或16、(1)(2)17、(1),令,则,∴,∴该厂从第3年开始盈利.(2)按方案①,年平均利润为, ,当且仅当时取等号,∴当时,取最大值16,∴第6年出售该厂时,可盈利(万元).5按方案②,,当时,取最大值128,∴第10年出售该厂时,可盈利(万元).两种方案虽然盈利总额相同,但方案①时间短,∴方案①更合理.18、解.(1)由c1有(0,1)B)21,23(),21,0(,MH设E:22221(0,0),xyabMEab在上,2222221123111442aabbab则解得122:22yxE(2))2,23(),2,0(),,0(),0,(1ccMcHcBcF设E22222422222221(0,0),,38403144abcxyabeeccabab即2),(32222eee舍或为常数19、解:(1)由题可知则;6(2)由(1)令,当且仅当取等号,此时则最大值为;(3)由题可知,不等式在上恒成立,即上恒成立即...