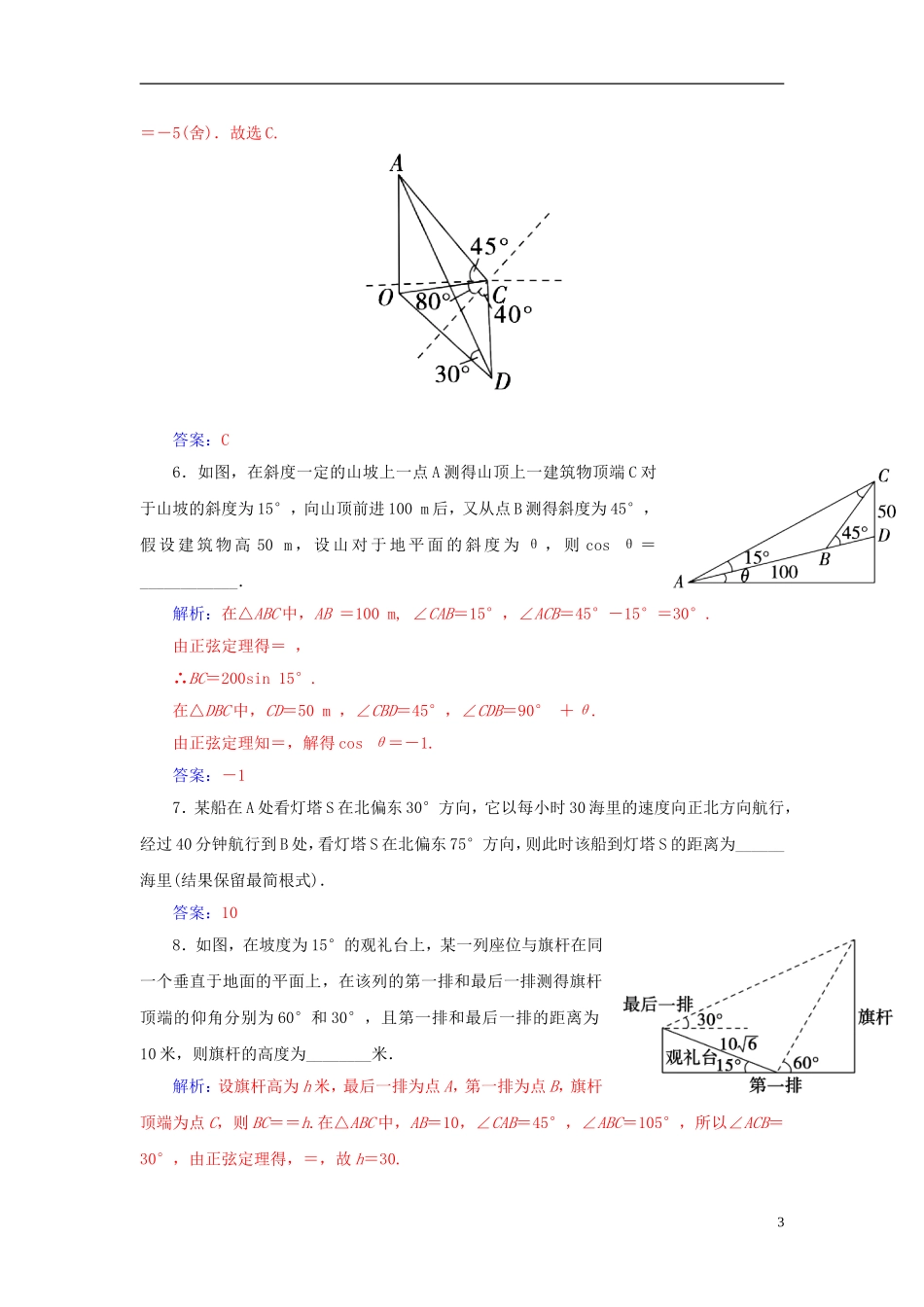
第八节解三角形的应用题号12345答案1.(2013·绍兴模拟)有一长为1的斜坡,它的倾斜角为20°,现高不变,将倾斜角改为10°,则斜坡长为()A.1B.2sin10°C.2cos10°D.cos20°解析:如图,∠ABC=20°,AB=1,∠ADC=10°,∴∠ABD=160°.在△ABD中,由正弦定理得=,∴AD=AB·==2cos10°.故选C.答案:C2.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为()A.锐角三角形B.直角三角形C.钝角三角形D.由增加的长度决定解析:设增加同样的长度为x,原三边长为a、b、c,且c2=a2+b2,a+b>c.新的三角形的三边长为a+x、b+x、c+x,知c+x为最大边,其对应角最大.而(a+x)2+(b+x)2-(c+x)2=x2+2(a+b-c)x>0,由余弦定理知新的三角形的最大角的余弦值为正,则为锐角,那么它为锐角三角形.答案:A3.台风中心从A地以每小时20km的速度向东北方向移动,离台风中心30km内的地区为危险区,城市B在A的正东方向40km处,B城市处于危险区内的时间为()A.0.5小时B.1小时C.1.5小时D.2小时解析:设A地东北方向上点P到B的距离为30km,AP=x,在△ABP中,PB2=AP2+AB2-2AP·ABcosA,1即302=x2+402-2x·40cos45°.化简得x2-40x+700=0.设该方程的两根为x1,x2,则|x1-x2|2=(x1+x2)2-4x1x2=400,∴|x1-x2|=20,即CD=20.故t===1.故选B.答案:B4.甲船在岛B的正南方A处,AB=10千米,甲船以每小时4千米的速度向正北航行,同时乙船自B出发以每小时6千米的速度向北偏东60°的方向驶去,当甲、乙两船相距最近时,它们所航行的时间是()A.分钟B.分钟C.21.5分钟D.2.15分钟解析:t小时后,甲、乙两船的距离为s,s2=(6t)2+(10-4t)2-2×6t×(10-4t)·cos120°=28t2-20t+100.∴当t==(小时)=×60=(分钟)时,甲、乙两船的距离最近.故选A.答案:A5.某人在C点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°方向前进10米到D,测得塔顶A的仰角为30°,则塔高为()A.15米B.5米C.10米D.12米解析:如图,设塔高为h,在Rt△AOC中,∠ACO=45°,则OC=OA=h.在Rt△AOD中,∠ADO=30°,则OD=h,在△OCD中,∠OCD=120°,CD=10,由余弦定理得:OD2=OC2+CD2-2OC·CDcos∠OCD,即(h)2=h2+102-2h×10×cos120°,∴h2-5h-50=0,解得h=10或h2=-5(舍).故选C.答案:C6.如图,在斜度一定的山坡上一点A测得山顶上一建筑物顶端C对于山坡的斜度为15°,向山顶前进100m后,又从点B测得斜度为45°,假设建筑物高50m,设山对于地平面的斜度为θ,则cosθ=____________.解析:在△ABC中,AB=100m,∠CAB=15°,∠ACB=45°-15°=30°.由正弦定理得=,∴BC=200sin15°.在△DBC中,CD=50m,∠CBD=45°,∠CDB=90°+θ.由正弦定理知=,解得cosθ=-1.答案:-17.某船在A处看灯塔S在北偏东30°方向,它以每小时30海里的速度向正北方向航行,经过40分钟航行到B处,看灯塔S在北偏东75°方向,则此时该船到灯塔S的距离为______海里(结果保留最简根式).答案:108.如图,在坡度为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆顶端的仰角分别为60°和30°,且第一排和最后一排的距离为10米,则旗杆的高度为________米.解析:设旗杆高为h米,最后一排为点A,第一排为点B,旗杆顶端为点C,则BC==h.在△ABC中,AB=10,∠CAB=45°,∠ABC=105°,所以∠ACB=30°,由正弦定理得,=,故h=30.3答案:309.某炮兵阵地位于地面A处,两观察所分别位于地面C和D处,已知CD=6km,∠ACD=45°,∠ADC=75°,目标出现于地面B处时,测量得∠BCD=30°,∠BDC=15°,如图,求炮兵阵地到目标的距离.解析:在△ACD中,∠CAD=180°-∠ACD-∠ADC=60°,CD=6,∠ACD=45°,根据正弦定理有AD==CD.同理,在△BCD中,∠CBD=180°-∠BCD-∠BDC=135°,CD=6,∠BCD=30°,根据正弦定理得BD==CD.又在△ABD中,∠ADB=∠ADC+∠BDC=90°,根据勾股定理有AB==CD=CD=(km).所以炮兵阵地到目标的距离为km.10.如图,矩形ABCD是机器人踢足球的场地,BA=170cm,AD=80cm,...