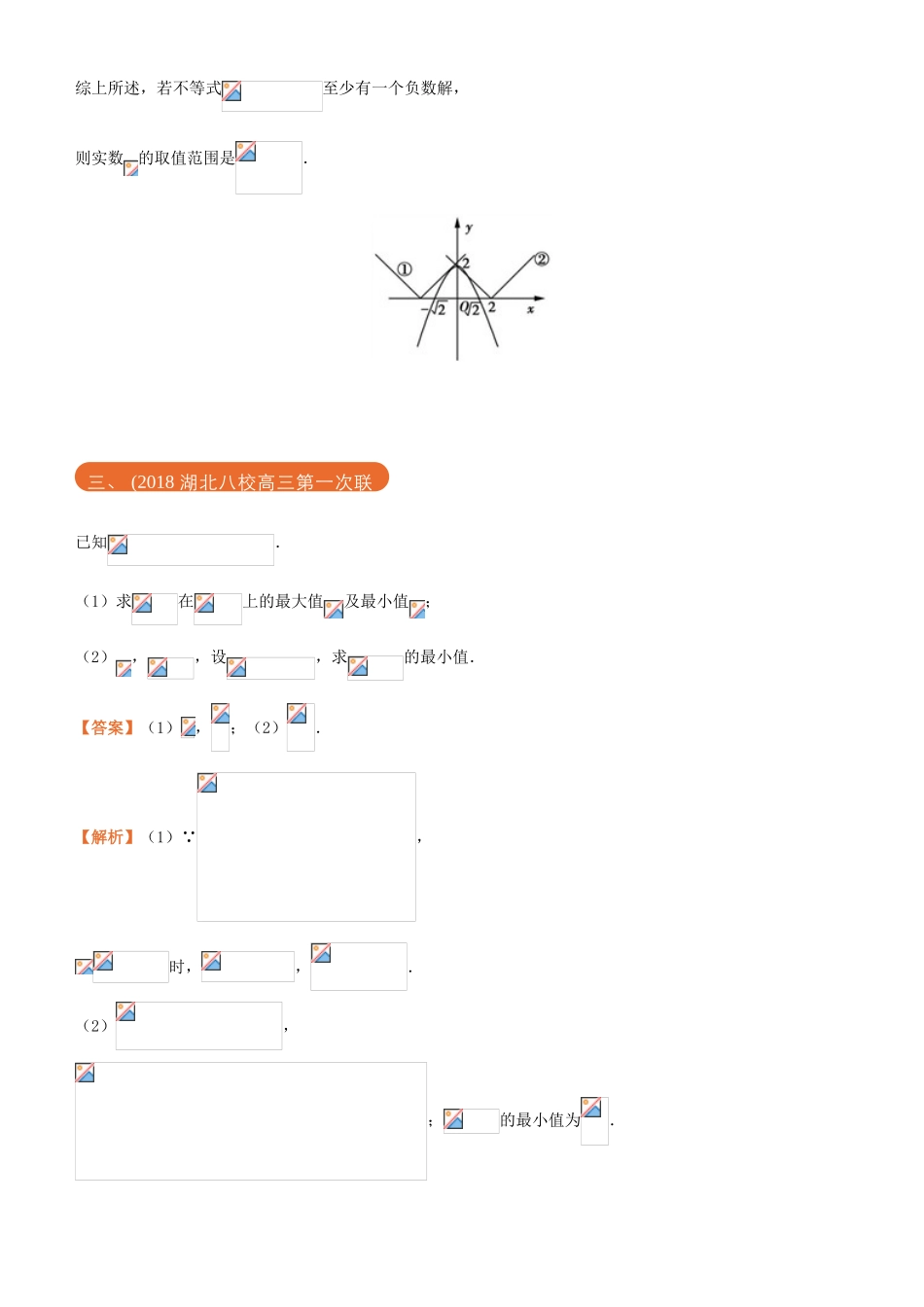
不等式选讲已知函数.(1)求不等式的解集;(2)若对恒成立,求的取值范围.【答案】(1);(2).【解析】(1)因为,所以当时,由得;当时,由得;当时,由得,综上,的解集为;(2)【方法一】由得,因为,当且仅当取等号,所以当时,取得最小值.所以,当时,取得最小值,故,即的取值范围为.【方法二】设,则,当时,的取得最小值,一、(2018广西高三下学期第二次模拟考试)所以当时,取得最小值,故,即的取值范围为.已知函数,.(1)若,解不等式;(2)若不等式至少有一个负数解,求实数的取值范围.【答案】(1).(2).【解析】(1)若,则不等式化为.当时,,即,不成立;当时,,即,解得.综上,不等式的解集为.(2)作出的图象如图所示,当时,的图象如折线①所示,由得,若相切,则,得,数形结合知,当时,不等式无负数解,则.当时,满足至少有一个负数解.当时,的图象如折线②所示,此时当时恰好无负数解,数形结合知,当时,不等式无负数解,则.二、(2018四川广元高三下学期第二次统考)综上所述,若不等式至少有一个负数解,则实数的取值范围是.已知.(1)求在上的最大值及最小值;(2),,设,求的最小值.【答案】(1),;(2).【解析】(1)∵,时,,.(2),;的最小值为.三、(2018湖北八校高三第一次联考)