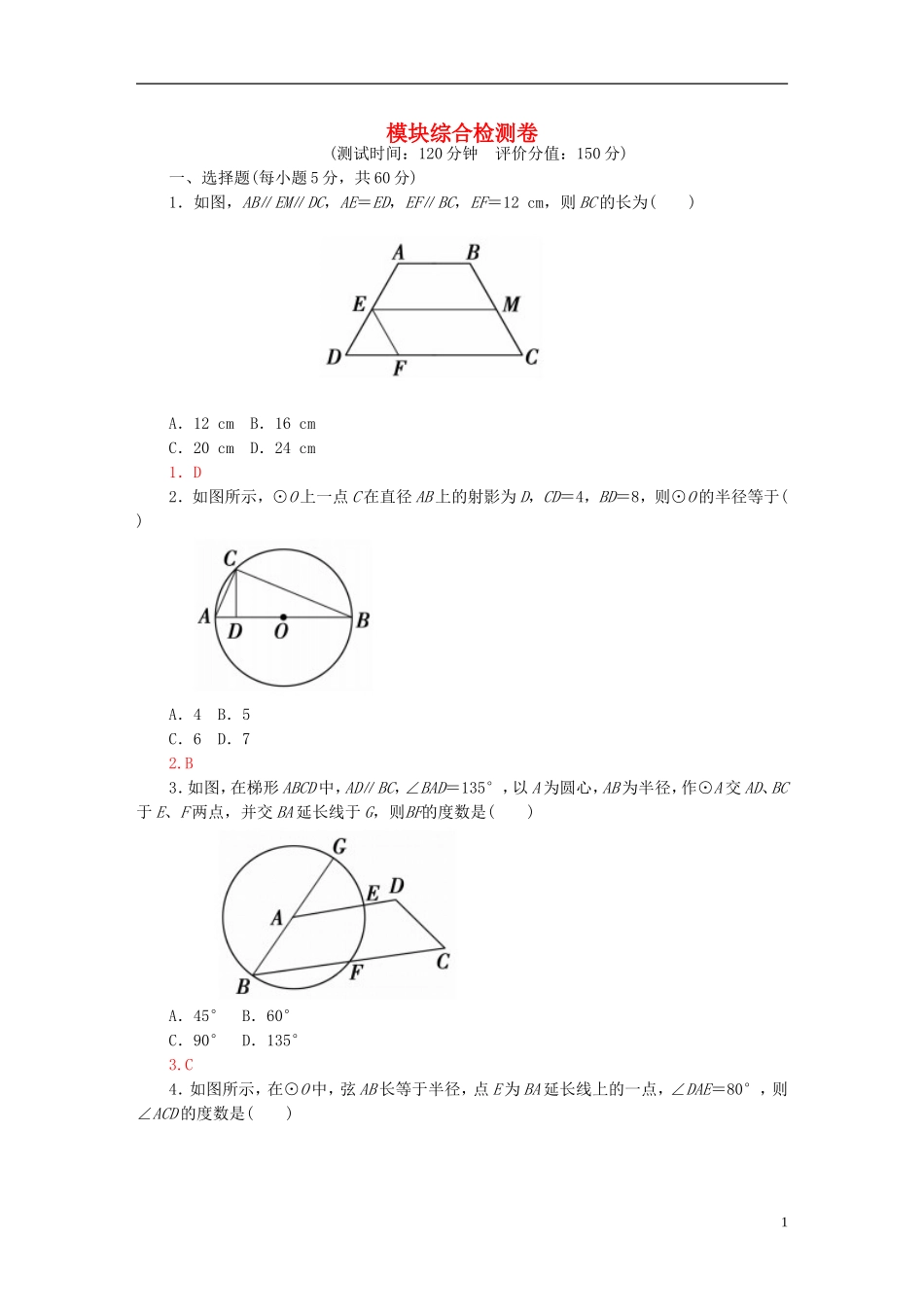
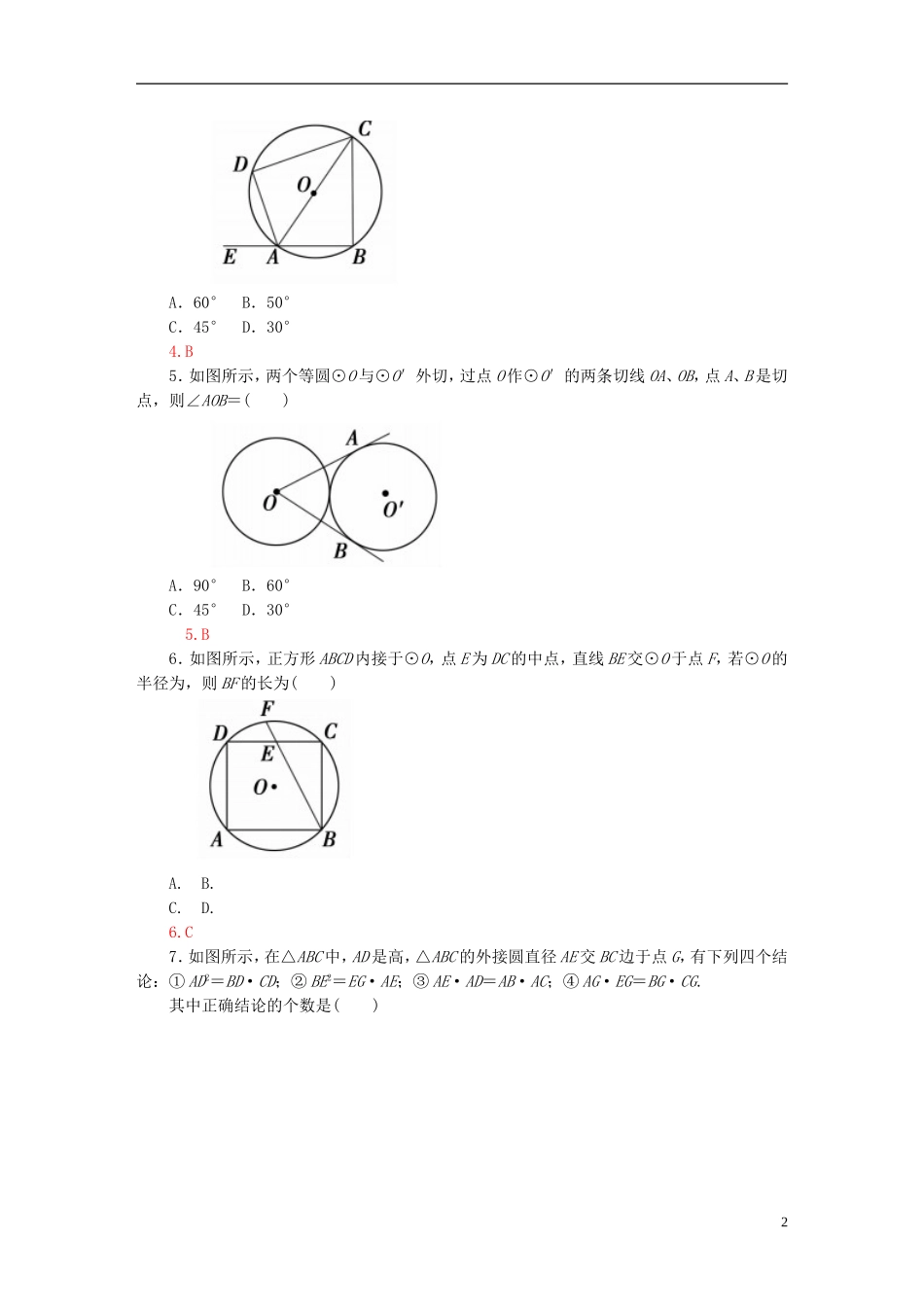
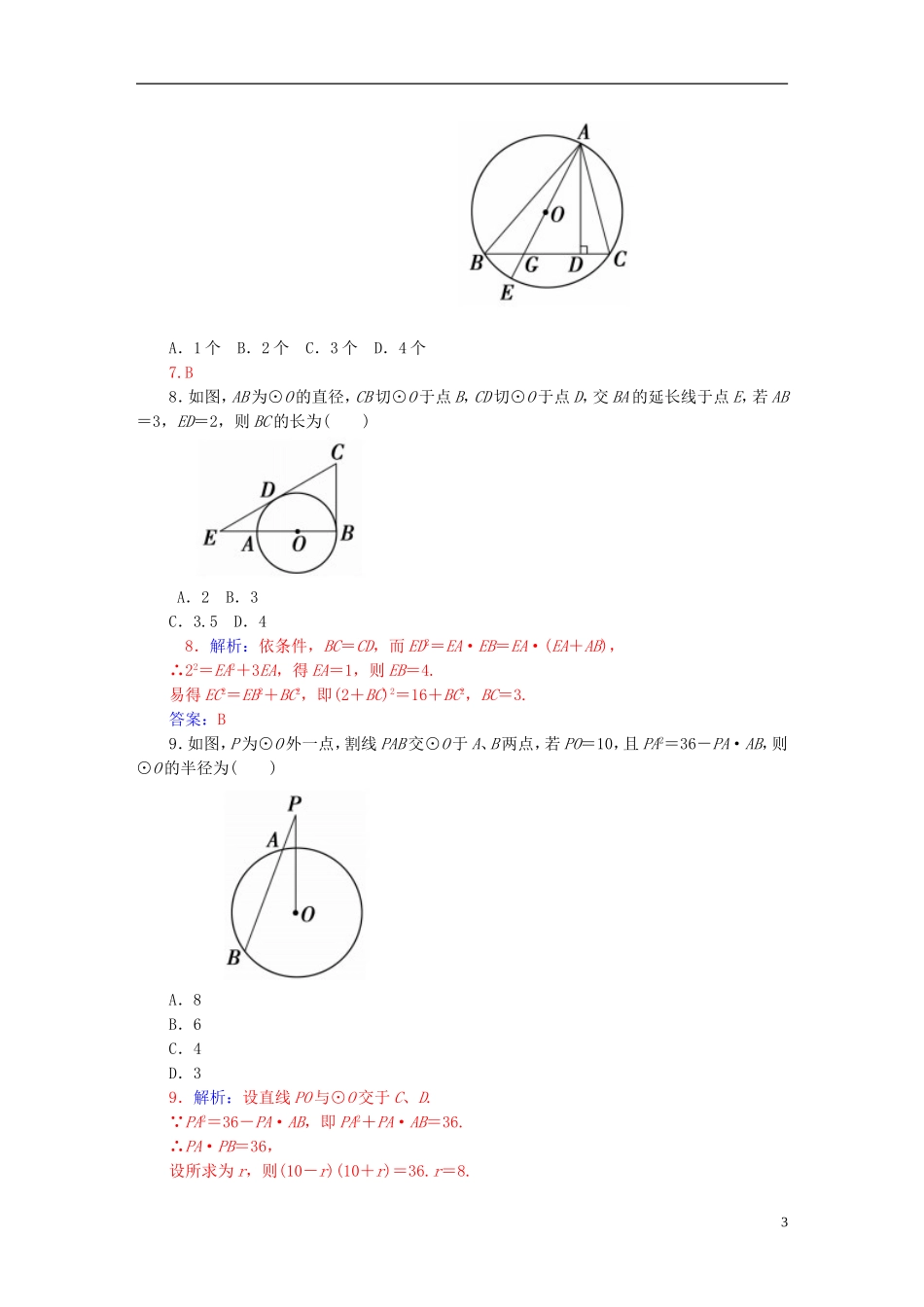
模块综合检测卷(测试时间:120分钟评价分值:150分)一、选择题(每小题5分,共60分)1.如图,AB∥EM∥DC,AE=ED,EF∥BC,EF=12cm,则BC的长为()A.12cmB.16cmC.20cmD.24cm1.D2.如图所示,⊙O上一点C在直径AB上的射影为D,CD=4,BD=8,则⊙O的半径等于()A.4B.5C.6D.72.B3.如图,在梯形ABCD中,AD∥BC,∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G,则BF的度数是()A.45°B.60°C.90°D.135°3.C4.如图所示,在⊙O中,弦AB长等于半径,点E为BA延长线上的一点,∠DAE=80°,则∠ACD的度数是()1A.60°B.50°C.45°D.30°4.B5.如图所示,两个等圆⊙O与⊙O′外切,过点O作⊙O′的两条切线OA、OB,点A、B是切点,则∠AOB=()A.90°B.60°C.45°D.30°5.B6.如图所示,正方形ABCD内接于⊙O,点E为DC的中点,直线BE交⊙O于点F,若⊙O的半径为,则BF的长为()A.B.C.D.6.C7.如图所示,在△ABC中,AD是高,△ABC的外接圆直径AE交BC边于点G,有下列四个结论:①AD2=BD·CD;②BE2=EG·AE;③AE·AD=AB·AC;④AG·EG=BG·CG.其中正确结论的个数是()2A.1个B.2个C.3个D.4个7.B8.如图,AB为⊙O的直径,CB切⊙O于点B,CD切⊙O于点D,交BA的延长线于点E,若AB=3,ED=2,则BC的长为()A.2B.3C.3.5D.48.解析:依条件,BC=CD,而ED2=EA·EB=EA·(EA+AB),∴22=EA2+3EA,得EA=1,则EB=4.易得EC2=EB2+BC2,即(2+BC)2=16+BC2,BC=3.答案:B9.如图,P为⊙O外一点,割线PAB交⊙O于A、B两点,若PO=10,且PA2=36-PA·AB,则⊙O的半径为()A.8B.6C.4D.39.解析:设直线PO与⊙O交于C、D. PA2=36-PA·AB,即PA2+PA·AB=36.∴PA·PB=36,设所求为r,则(10-r)(10+r)=36.r=8.3答案:A10.一圆柱面与一平面相截,平面与母线所成的角为60°,截线上最长的弦为4,则圆柱面的半径为()A.B.2C.3D.610.C11.如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的中位线长是()A.10B.C.D.1211.解析:如图,作DE∥AC交BC的延长线于点E,所以四边形ACED是平行四边形,所以AD=CE.又因为AC⊥BD,所以DE⊥BD.在Rt△BED中,易求BE的长是=15.则此梯形的中位线长是.答案:C12.如图,AB=,BC=2,CD=1,∠ABC=45°,则四边形ABCD的面积为()A.B.C.D.12.解析:如图,连接AC、OD,则△ABC为等腰直角三角形,AC=,S△ABC=××=1.4又因为OD=OC=CD,所以△OCD为等边三角形,所以∠OCD=60°,所以∠ACD=60°-45°=15°,S△ADC=×AC×DCsin15°=,因此四边形ABCD的面积为答案:D二、填空题(每小题5分,共20分)13.如图,EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是________.13.99°14.如图,已知△ABC中,边AC上一点F分AC为=,BF上一点G分BF为=,AG的延长线与BC交于点E,则BE∶EC=________.14.15.(2015·惠州市高三第三次调研考试,理)如图所示,点A,B,C都在圆O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为________.16.如图,已知F为抛物线的焦点,l为其准线,过F引PQ⊥轴AB,交抛物线于P、Q,A在l5上,以PQ为直径作圆,C为l上一点,CF交⊙F于D.CA=4,CD=2,则PQ=________.16.解析:过P作PE⊥l,延长CF交⊙F与G. PF=PE,又PE=AF,即PF=AF.∴l为⊙F切线.∴CA2=CD·CG,即16=2(2+DG),DG=6,∴PQ=6.答案:6三、解答题(本大题共6题,共70分)17.(10分)如图所示,已知两同心圆中,大圆的弦AB、AC切小圆于D、E,△ABC的周长为12cm,求△ADE的周长.17.解析:连接OD、OE. AB、AC切小圆于D、E,∴OD⊥AB,OE⊥AC.∴AD=AB,AE=AC.又∠DAE=∠BAC,∴△ADE∽△ABC. △ABC的周长=AB+AC+BC=12(cm),∴△ADE的周长=×12=6(cm).故△ADE的周长为6cm.18.(12分)如图,△ABC为圆的内接三角形,BD为圆的弦,且BD∥AC.过点A作圆的切线与DB的延长线交于点E,AD=AC,AE=6,BD=5,求CF的长.18.解析:先证明四边形AEBC是平行四边形,然后利用切割线定理求出EB的长,即得AC...