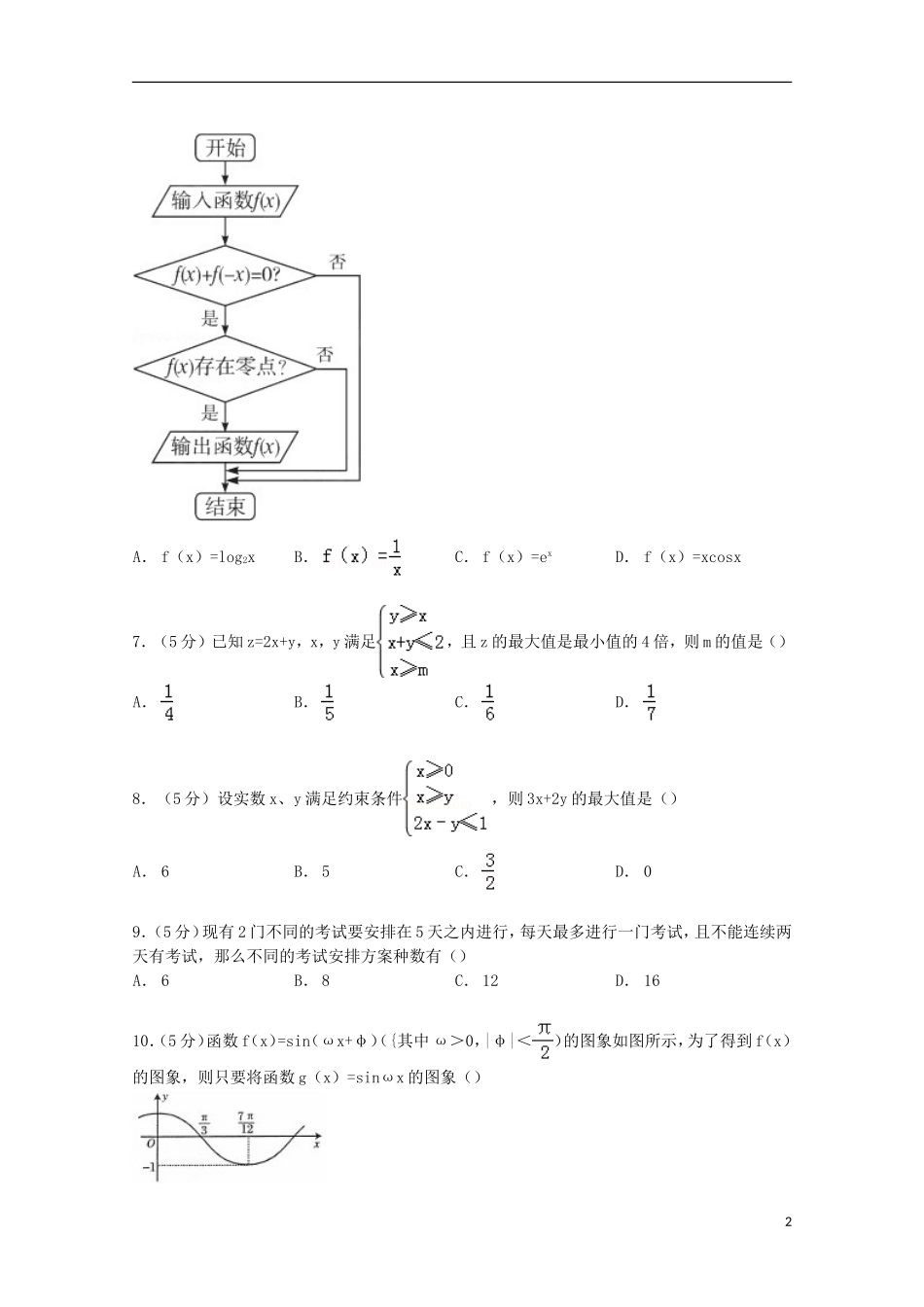
贵州省贵阳市2015届高三上学期8月摸底数学试卷(理科)一、选择题(共12小题,每小题5分,满分60分)1.(5分)复数z=3﹣2i,i是虚数单位,则z的虚部是()A.2iB.﹣2iC.2D.﹣22.(5分)若集合M={x|y=},N={x|y=log2(1﹣x)},则集合M∩N=()A.(﹣∞,1)B.(1,+∞)C.(0,1)D.R3.(5分)已知f(x)是定义在R上的奇函数,且x≥0时f(x)的图象如图所示,则f(﹣2)=()A.﹣3B.﹣2C.﹣1D.24.(5分)在△ABC中,角A、B、C的对边分别为a,b,c,a=1,b=,∠A=则∠B等于()A.B.C.或D.5.(5分)下列判断错误的是()A.“am2<bm2”是“a<b“的充分不必要条件B.命题“∈∀R,x3﹣x2﹣1≤0”的否定是“∃x∈R,x3﹣x2﹣1>0”C.命题“若α=,则tanα=1”的逆否命题是“若tanα≠1,则α≠”D.若p∧q为假命题,则p,q均为假命题6.(5分)某程序框图如图所示,现输入如下四个函数,则可以输出的函数是()1A.f(x)=log2xB.C.f(x)=exD.f(x)=xcosx7.(5分)已知z=2x+y,x,y满足,且z的最大值是最小值的4倍,则m的值是()A.B.C.D.8.(5分)设实数x、y满足约束条件,则3x+2y的最大值是()A.6B.5C.D.09.(5分)现有2门不同的考试要安排在5天之内进行,每天最多进行一门考试,且不能连续两天有考试,那么不同的考试安排方案种数有()A.6B.8C.12D.1610.(5分)函数f(x)=sin(ωx+φ)({其中ω>0,|φ|<)的图象如图所示,为了得到f(x)的图象,则只要将函数g(x)=sinωx的图象()2A.向右平移个单位B.向右平移个单位C.向左平移个单位D.向左平移个单位11.(5分)直线L过抛物线C:y2=2px(p>0)的焦点F且与C相交于A、B两点,且AB的中点M的坐标为(3,2),则抛物线C的方程为()A.y2=2x或y2=4xB.y2=4x或y2=8xC.y2=6x或y2=8xD.y2=2x或y2=8x12.(5分)设函数,其中[x]表示不超过x的最大整数,如[﹣1.2]=﹣2,[1.2]=1,[1]=1,若直线y=kx+k(k>0)与函数y=f(x)的图象恰有三个不同的交点,则k的取值范围是()A.B.C.D.二、填空题:本大题共4小题,每小题5分.13.(5分)设sinα=2cosα,则tan2α的值.14.(5分)(a+2x)5的展开式中,x2的系数等于40,则a等于.15.(5分)某几何体的三视图如图(其中侧视图中的圆弧是半圆),则该几何体的表面积为.16.(5分)边长为2的正方形ABCD,其内切圆与边BC切于点E、F为内切圆上任意一点,则•取值范围为.三、解答题:解答应写出文字说明,证明过程或演算步骤.17.(12分)数列{an}的通项公式为an=2n﹣1,数列{bn}是等差数列且b1=a1,b4=a1+a2+a3.(Ⅰ)求数列{bn}的通项公式;(Ⅱ)设Cn=,数列{cn}的前n项和为Tn,证明:Tn<.18.(12分)如图,在直三棱柱ABC﹣A1B1C1中,AB⊥BC,AB=BC=1,AA1=2,D是AA1的中点,E是B1C的中点,(1)证明:DE∥平面ABC(2)求二面角C﹣B1D﹣B的余弦值.319.(12分)交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10)严重拥堵.在晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的频率分布直方图如图所示.(1)在这20个路段中,轻度拥堵、中度拥堵的路段各有多少个?(2)从这20个路段中随机抽出3个路段,用X表示抽取的中度拥堵的路段的个数,求X的分布列及期望.20.(12分)如图,在平面直角坐标系xoy中,椭圆=1(a>b>0)的离心率为,过椭圆由焦点F作两条互相垂直的弦AB与CD.当直线AB斜率为0时,弦AB长4.(1)求椭圆的方程;(2)若|AB|+|CD|=.求直线AB的方程.21.(12分)已知函数f(x)=axlnx(a∈R)在x=e处的切线斜率为2.(1)求f(x)的最小值;4(2)设A(x1,f(x1))与B(x2,f(x2))(x1<x2)是函数y=f(x)图象上的两点,直线AB的斜率为k,函数f(x)的导函数为f′(x),若存在x0>0,使f′(x0)=k.求证:x2>x0.22.(10分)如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C...