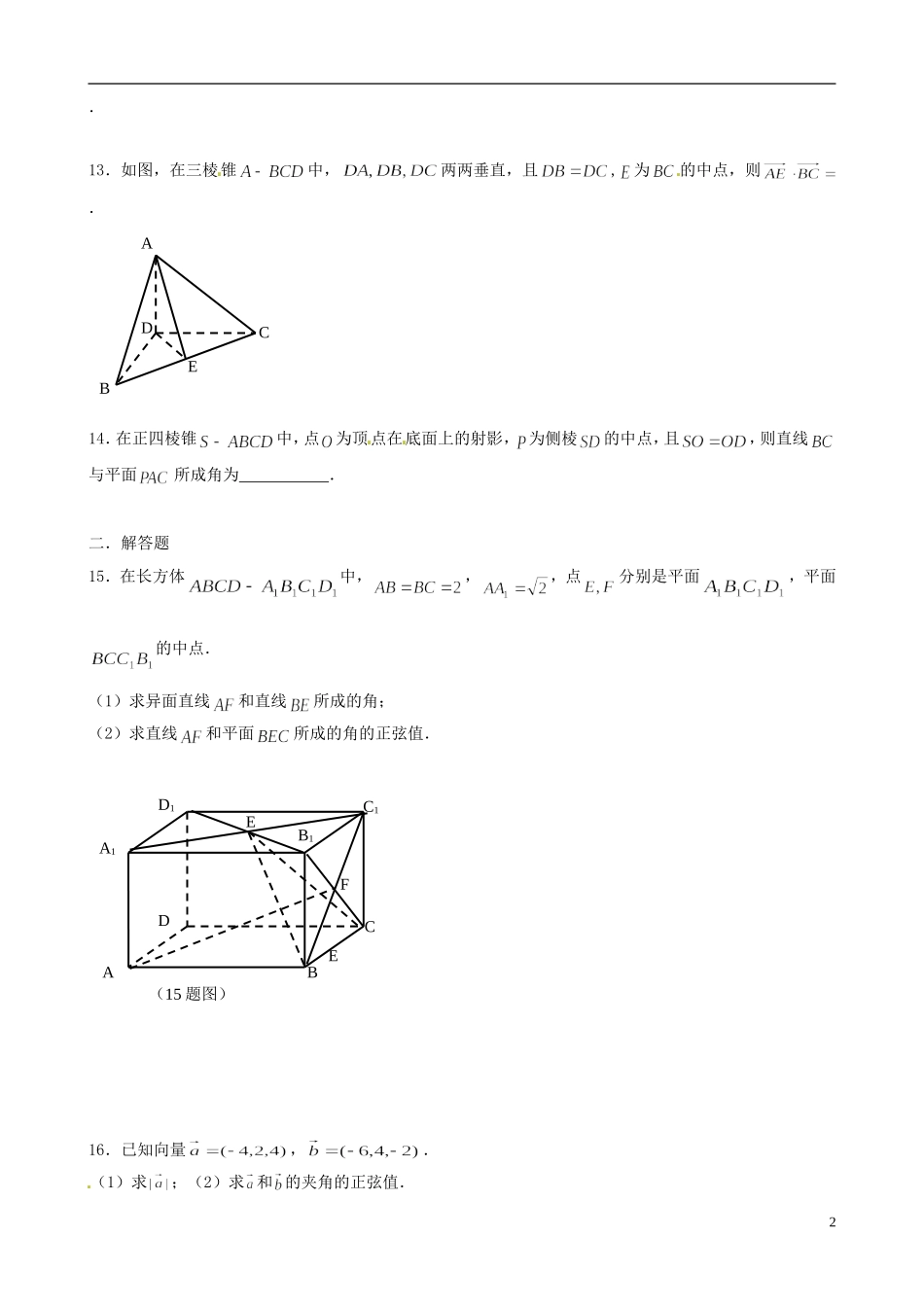
江苏省连云港市赣榆县海头高级中学高中数学上学期冲刺期末市统考专题复习专题14空间向量新人教A版必修3一.填空题.1.在正方体中,若点是侧面的中心,且,则.2.已知向量,,且与互相垂直,则.3.已知向量,,则.4.已知点,,三点共线,则.5.已知的三个顶点的坐标分别为,,,则角的大小为.6.直线的方向向量,平面的法向量,若直线,则.7.已知直线过点,,且是直线的方向向量,则.8.已知向量,分别是直线的方向向量和平面的法向量,若,则直线和平面所成角的大小为.9.已知过点的直线的方向向量平行于向量,平面过直线与点,则下列向量中,平面的法向量不可能是.(填序号)(1);(2);(3);(4)10.在正方体中,正方形的中心为点O,则平面与平面的夹角的大小为.11.在直三棱柱中,,,点为上一点,若二面角的大小为,则的长为.12.正四面体中,,,则直线和直线的夹角的余弦值为1.13.如图,在三棱锥中,两两垂直,且,为的中点,则.14.在正四棱锥中,点为顶点在底面上的射影,为侧棱的中点,且,则直线与平面所成角为.二.解答题15.在长方体中,,,点分别是平面,平面的中点.(1)求异面直线和直线所成的角;(2)求直线和平面所成的角的正弦值.16.已知向量,.(1)求;(2)求和的夹角的正弦值.ABCDE(15题图)ABCDD1A1B1C1EEF217.如图,四棱锥的底面是正方形,每条侧棱长都是底面边长的倍,点为侧棱上的点.(1)求证:;(2)若平面,则侧棱上是否存在一点,使得平面.若存在,求的值;若不存在,请说明理由.18.如图,在三棱柱ABC-A1B1C1中,BA⊥AC,AB=AC=A1B=2,顶点A1在底面ABC上的射影恰为点B.(1)求异面直线AA1与BC所成角的大小;(2)在棱B1C1上确定一点P,使AP=,并求出二面角P-AB-A1的平面角的余弦值.SABCDP3C1B1BACA1(第18题)4