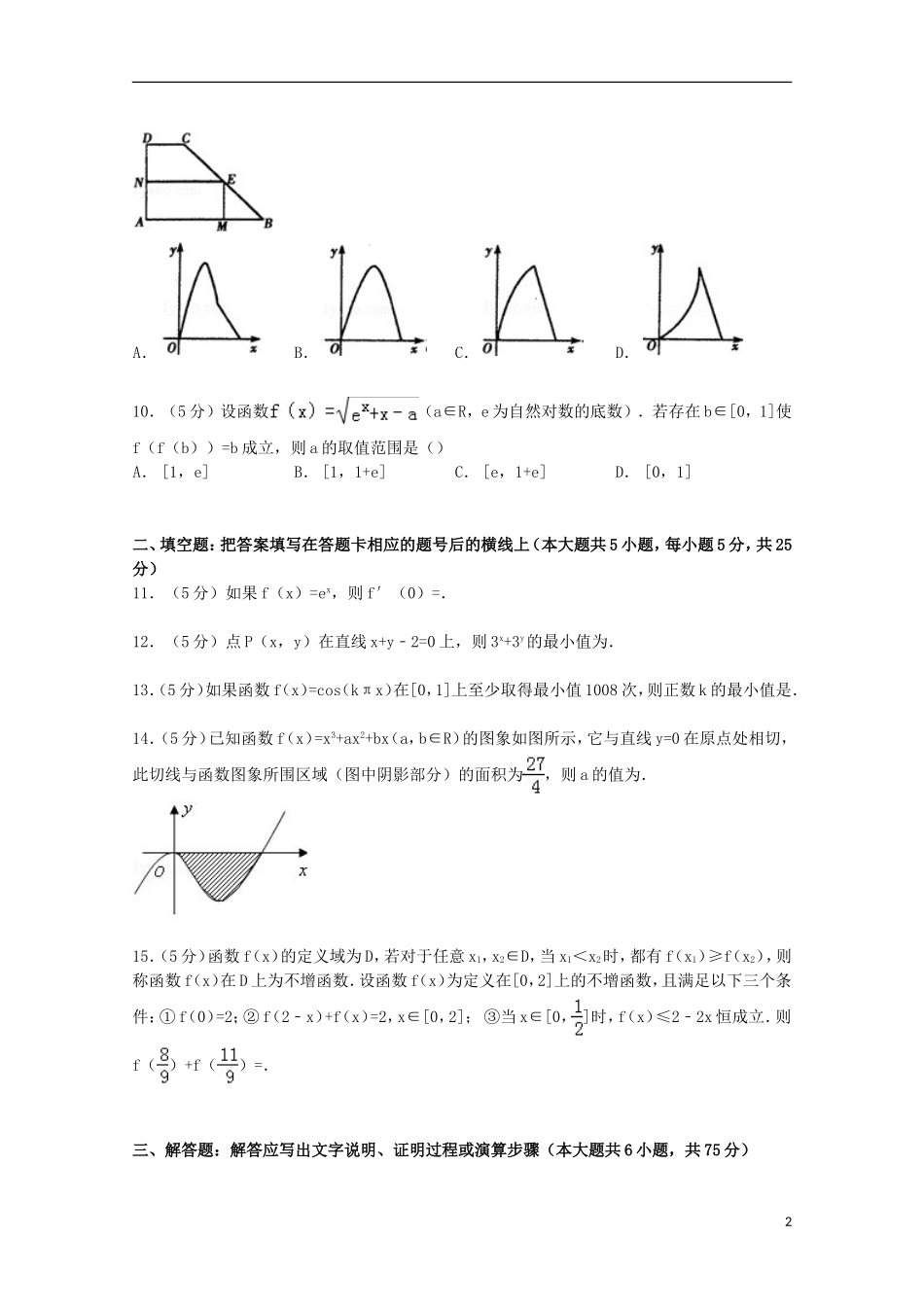
江西省南昌三中2015届高三上学期第二次月考数学试卷(理科)一.选择题1.(5分)已知集合M={x|y=},N={x|y=log2(2﹣x)},则∁R(M∩N)()A.[1,2)B.(﹣∞,1)∪[2,+∞)C.[0,1]D.(﹣∞,0)∪[2,+∞)2.(5分)若a=3sin60,b=log3cos60°,c=log3tan60°,则()A.a>b>cB.a>c>bC.c>b>aD.b>a>c3.(5分)若函数y=f(x)的定义域是[0,2],则函数的定义域是()A.[0,1]B.[0,1)C.[0,1)∪(1,4]D.(0,1)4.(5分)设x、y是两个实数,命题“x、y中至少有一个数大于1”成立的充分不必要条件是()A.x+y=2B.x+y>2C.x2+y2>2D.xy>15.(5分)设函数f(x)=3sin(2x+)+1,将y=f(x)的图象向右平移φ(φ>0)个单位,使得到的图象关于y轴对称,则φ的最小值为()A.B.C.D.6.(5分)若,,均为单位向量,且=0,则|+﹣|的最小值为()A.B.1C.+1D.7.(5分)已知θ∈(0,),满足cosθcos2θcos4θ=的θ共有()个.A.1B.2C.3D.48.(5分)设实数x,y满足约束条件,且目标函数z=ax+by(a>0,b>0)的最大值为1,则+的最小值为()A.4B.8C.9D.69.(5分)如图,直角梯形ABCD中,∠A=90°,∠B=45°,底边AB=5,高AD=3,点E由B沿折线BCD向点D移动,EM⊥AB于M,ENAD于N,设BM=x,矩形AMEN的面积为y,那么y与x的函数关系的图象大致是()1A.B.C.D.10.(5分)设函数(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是()A.[1,e]B.[1,1+e]C.[e,1+e]D.[0,1]二、填空题:把答案填写在答题卡相应的题号后的横线上(本大题共5小题,每小题5分,共25分)11.(5分)如果f(x)=ex,则f′(0)=.12.(5分)点P(x,y)在直线x+y﹣2=0上,则3x+3y的最小值为.13.(5分)如果函数f(x)=cos(kπx)在[0,1]上至少取得最小值1008次,则正数k的最小值是.14.(5分)已知函数f(x)=x3+ax2+bx(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为,则a的值为.15.(5分)函数f(x)的定义域为D,若对于任意x1,x2∈D,当x1<x2时,都有f(x1)≥f(x2),则称函数f(x)在D上为不增函数.设函数f(x)为定义在[0,2]上的不增函数,且满足以下三个条件:①f(0)=2;②f(2﹣x)+f(x)=2,x∈[0,2];③当x∈[0,]时,f(x)≤2﹣2x恒成立.则f()+f()=.三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6小题,共75分)216.(12分)记函数f(x)=的定义域为A,g(x)=lg[(1﹣x)(x+1)]的定义域为B,求集合A、B、A∩B.17.(12分)在△ABC中,a,b,c分别是角A,B,C的对边,且(2a+c)cosB=﹣bcosC.(Ⅰ)求角B的大小;(Ⅱ)若b=2,a+c=4,求△ABC的面积.18.(12分)一个盒子装有六张卡片,上面分别写着如下六个函数:f1(x)=x,f2(x)=x2,f3(x)=x3,f4(x)=x4,f5(x)=xcosx,f6(x)=xsinx.(Ⅰ)从中任意拿取2张卡片,其中至少有一张卡片上写着的函数为奇函数,在此条件下求两张卡片上写着的函数相加得到的新函数为奇函数的概率;(Ⅱ)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张写有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.19.(12分)如图,在底面是菱形的四棱锥P﹣ABCD中,∠ABC=60°,PA=AC=a,PB=PD=,点E在PD上,且PE:ED=2:1.(Ⅰ)证明PA⊥平面ABCD;(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小;(Ⅲ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.20.(13分)设a为实数,函数f(x)=x2+|x﹣a|+1,x∈R(1)讨论f(x)的奇偶性;(2)求f(x)的最小值.21.(14分)已知函数(a为实常数).(Ⅰ)当a=1时,求函数g(x)=f(x)﹣2x的单调区间;(Ⅱ)若函数f(x)在区间(0,2)上无极值,求a的取值范围;(Ⅲ)已知n∈N*且n≥3,求证:.江西省南昌三中2015届高三上学期第二次月考数学试卷(理科)参考答案与试题解析3一.选择题1.(5分)已知集合M={x|y=},N={x|y=log2(2﹣x)},则∁R(M∩N)()A.[1,...