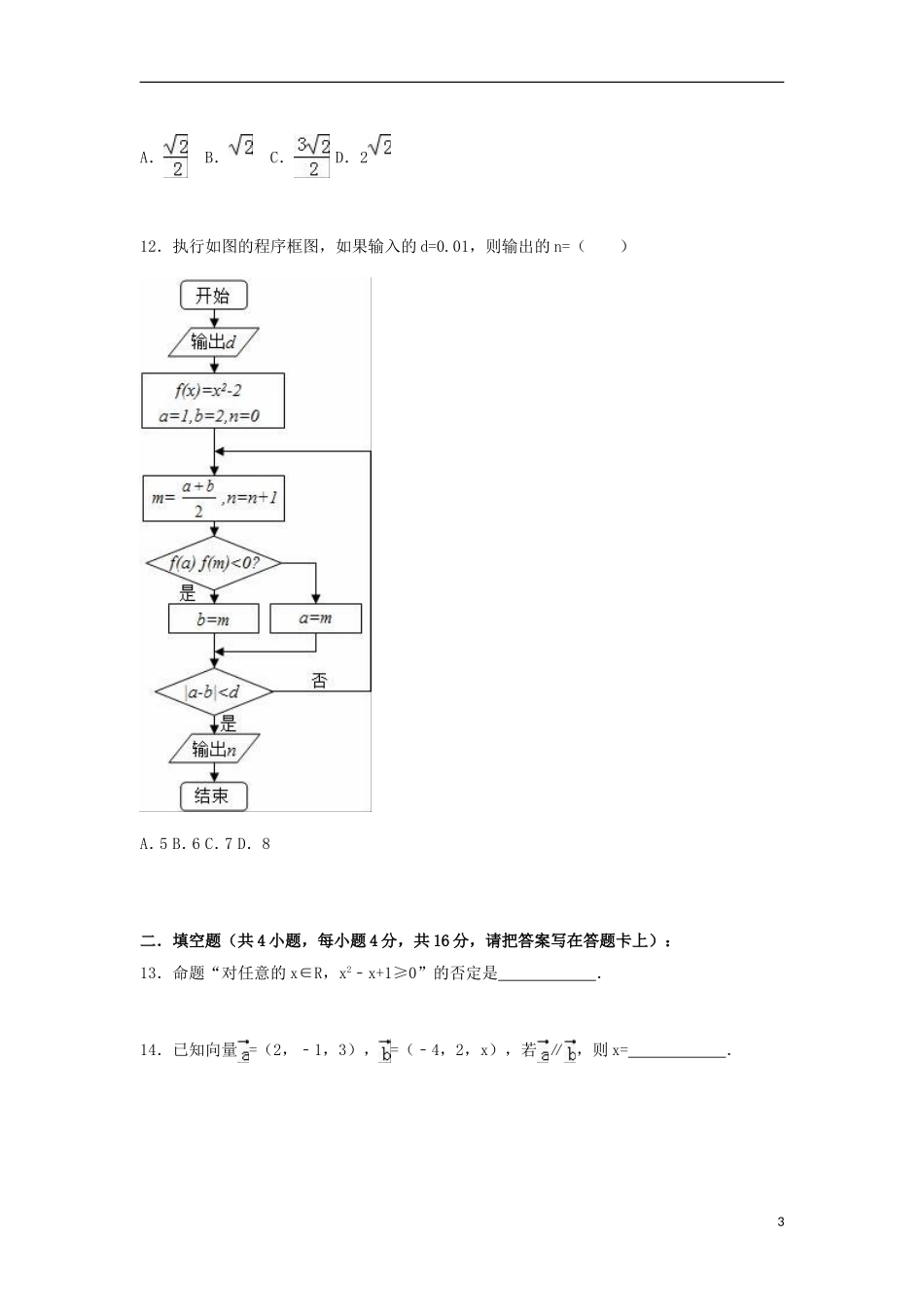
2015-2016学年福建省泉州市南安一中高二(上)期中数学试卷(理科)一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求):1.双曲线2x2﹣y2=8的实轴长是()A.4B.4C.2D.22.已知p:2+2=5,q:3≥2,则下列判断中,错误的是()A.p或q为真,非q为假B.p或q为真,非p为真C.p且q为假,非p为假D.p且q为假,p或q为真3.抛物线的焦点坐标是()A.(﹣2,0)B.(2,0)C.D.4.根据下列算法语句,当输入x为60时,输出y的值为()A.25B.30C.31D.615.若椭圆+=1的两个焦点F1,F2,M是椭圆上一点,且|MF1|﹣|MF2|=1,则△MF1F2是()A.钝角三角形B.直角三角形C.锐角三角形D.等边三角形16.对于常数m、n,“mn>0”是“方程mx2+ny2=1的曲线是椭圆”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件7.若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是()A.B.C.D.8.有下列四个命题:①“若x+y=0,则x,y互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若q≤1,则x2+2x+q=0有实根”的逆命题;④“若x+y≠3,则x≠1或y≠2”,其中真命题有()A.①②B.②③C.①③D.①③④9.若向量=(1,λ,2),=(2,﹣1,2),且与的夹角余弦值为,则λ等于()A.2B.﹣2C.﹣2或D.2或﹣10.双曲线C的中心在原点,焦点在x轴,离心率e=,C与抛物线y2=16x的准线交于A,B点,|AB|=4,则C的实轴长为()A.B.2C.4D.811.过抛物线y2=4x的焦点F的直线交抛物线于A,B两点,点O是原点,若|AF|=3,则△AOF的面积为()2A.B.C.D.212.执行如图的程序框图,如果输入的d=0.01,则输出的n=()A.5B.6C.7D.8二.填空题(共4小题,每小题4分,共16分,请把答案写在答题卡上):13.命题“对任意的x∈R,x2﹣x+1≥0”的否定是.14.已知向量=(2,﹣1,3),=(﹣4,2,x),若∥,则x=.315.已知双曲线的渐近线方程为y=±x,且过点M(﹣1,3),则该双曲线的标准方程为.16.若二进制数100y011和八进制数x03相等,则x+y=.三.解答题(本大题共6小题,共74分):17.已知双曲线﹣=1的右焦点与抛物线y2=12x的焦点重合,求该双曲线的焦点到其渐近线的距离.18.命题p:“方程+=1表示双曲线”(k∈R);命题q:y=log2(kx2+kx+1)定义域为R,若命题p∨q为真命题,p∧q为假命题,求实数k的取值范围.19.如图,棱锥P﹣ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=.(1)求证:BD⊥平面PAC;(2)求二面角P﹣CD﹣B余弦值的大小;(3)求点C到平面PBD的距离.20.椭圆C:+y2=1,直线l交椭圆C于A,B两点.4(1)若l过点P(1,)且弦AB恰好被点P平分,求直线l方程.(2)若l过点Q(0,2),求△AOB(O为原点)面积的最大值.21.如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2)(Ⅰ)当λ=1时,证明:直线BC1∥平面EFPQ;(Ⅱ)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.22.如图,椭圆E:的左焦点为F1,右焦点为F2,离心率e=.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.(Ⅰ)求椭圆E的方程.(Ⅱ)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.562015-2016学年福建省泉州市南安一中高二(上)期中数学试卷(理科)参考答案与试题解析一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合题目要求):1.双曲线2x2﹣y2=8的实轴长是()A.4B.4C.2D.2【考点】双曲线的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】双曲线方程化为标准方程,即可确定实轴长.【解答】解:双曲线2x2﹣y2=8,可化为∴a=2,∴双曲线2x2﹣y2=8的实轴长是4故选B.【点评】本题考查双曲线的几何性质,考查学生的计算能力,属于...