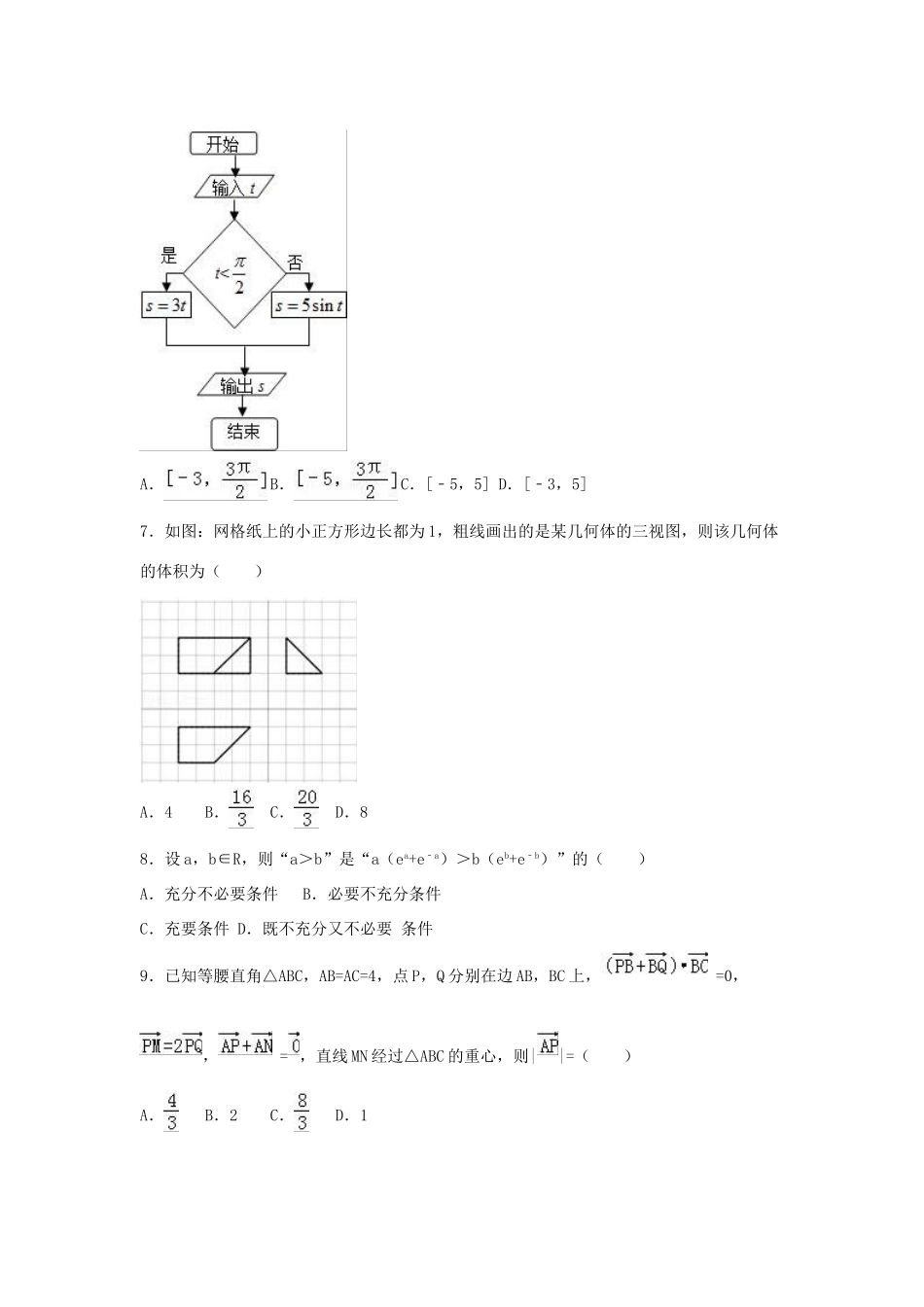
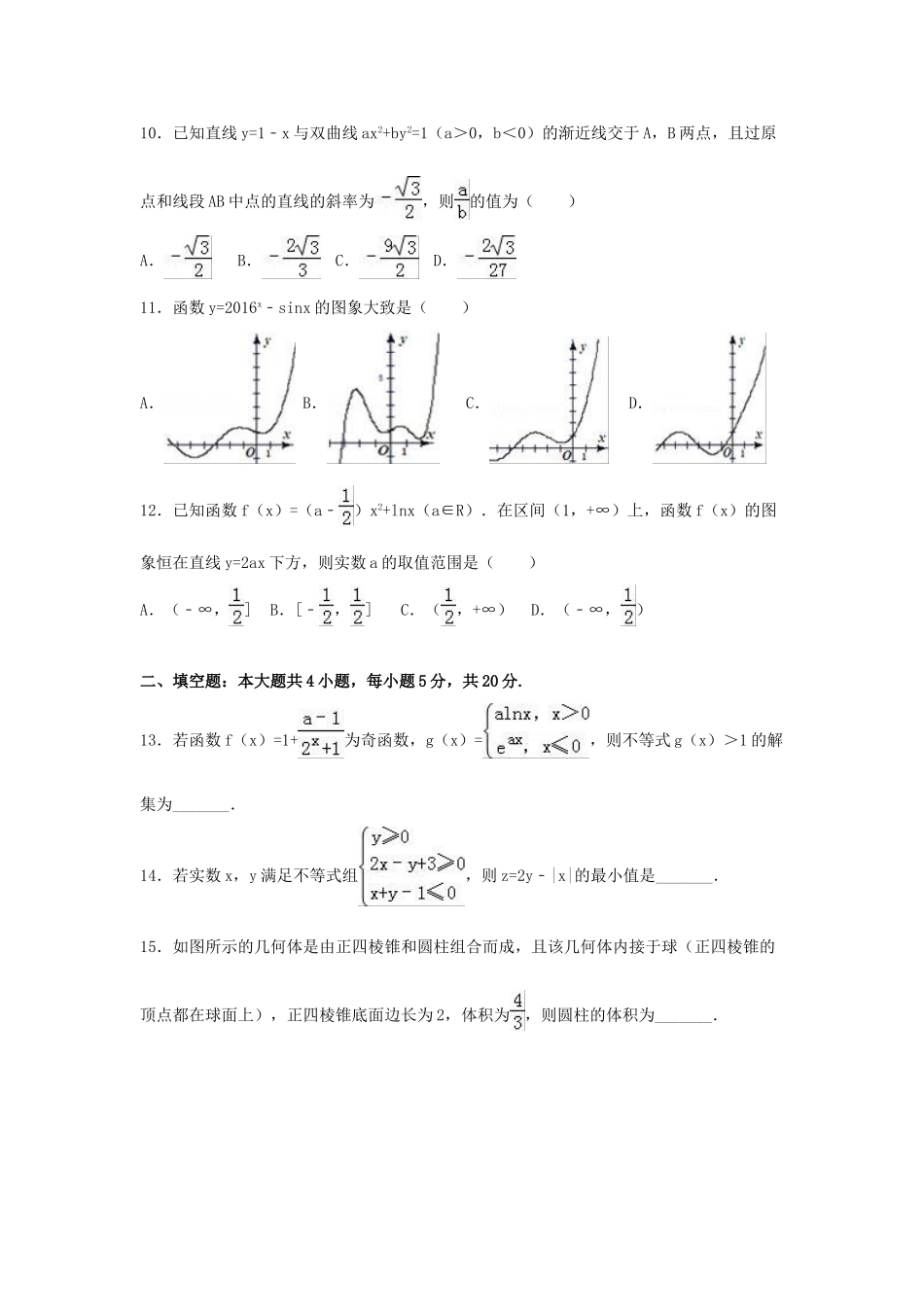
2016年江西省五市八校高考数学二模试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是满足题目要求的.)1.设集合A={x|2x﹣1>5},集合B={x|y=lg(6﹣x)},则A∩B等于()A.(3,6)B.[3,6]C.(3,6]D.[3,6)2.设i是虚数单位,若复数a﹣(a∈R)是纯虚数,则a的值为()A.B.﹣2C.2D.3.(2x+5y)2016展开式中第k+1项的系数为()A.B.C.D.4.已知正数m是2和8的等比中项,则圆锥曲线x2+=1的焦点坐标为()A.B.C.或D.或5.等差数列{an}的公差d<0且,则数列{an}的前n项和sn有最大值,当sn取得最大值时的项数n是()A.6B.7C.5或6D.6或76.执行如图的程序框图,如果输入的t∈[﹣1,π],则输出的S属于()A.B.C.[﹣5,5]D.[﹣3,5]7.如图:网格纸上的小正方形边长都为1,粗线画出的是某几何体的三视图,则该几何体的体积为()A.4B.C.D.88.设a,b∈R,则“a>b”是“a(ea+e﹣a)>b(eb+e﹣b)”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件9.已知等腰直角△ABC,AB=AC=4,点P,Q分别在边AB,BC上,=0,,=,直线MN经过△ABC的重心,则||=()A.B.2C.D.110.已知直线y=1﹣x与双曲线ax2+by2=1(a>0,b<0)的渐近线交于A,B两点,且过原点和线段AB中点的直线的斜率为,则的值为()A.B.C.D.11.函数y=2016x﹣sinx的图象大致是()A.B.C.D.12.已知函数f(x)=(a﹣)x2+lnx(a∈R).在区间(1,+∞)上,函数f(x)的图象恒在直线y=2ax下方,则实数a的取值范围是()A.(﹣∞,]B.[﹣,]C.(,+∞)D.(﹣∞,)二、填空题:本大题共4小题,每小题5分,共20分.13.若函数f(x)=1+为奇函数,g(x)=,则不等式g(x)>1的解集为_______.14.若实数x,y满足不等式组,则z=2y﹣|x|的最小值是_______.15.如图所示的几何体是由正四棱锥和圆柱组合而成,且该几何体内接于球(正四棱锥的顶点都在球面上),正四棱锥底面边长为2,体积为,则圆柱的体积为_______.16.己知数列{an}是等差数列,数列{bn}是等比数列,对一切n∈N*,都有=bn,则数列{bn}的通项公式为_______.三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.设△ABC的三个内角A,B,C所对的边分别为a,b,c,点O为△ABC的外接圆的圆心,若满足a+b≥2c.(1)求角C的最大值;(2)当角C取最大值时,己知a=b=,点P为△ABC外接圆圆弧上﹣点,若,求x•y的最大值.18.骨质疏松症被称为“静悄悄的流行病“,早期的骨质疏松症患者大多数无明显的症状,针对中学校园的学生在运动中骨折事故频发的现状,教师认为和学生喜欢喝碳酸饮料有关,为了验证猜想,学校组织了一个由学生构成的兴趣小组,联合医院检验科,从高一年级中按分层抽样的方法抽取50名同学(常喝碳酸饮料的同学30,不常喝碳酸饮料的同学20),对这50名同学进行骨质检测,检测情况如表:(单位:人)有骨质疏松症状无骨质疏松症状总计常喝碳酸饮料的同学22830不常喝碳酸饮料的同学81220总计302050(1)能否据此判断有97.5%的把握认为骨质疏松症与喝碳酸饮料有关?(2)现从常喝碳酸饮料且无骨质疏松症状的8名同学中任意抽取两人,对他们今后是否有骨质疏松症状情况进行全程跟踪研究,记甲、乙两同学被抽到的人数为X,求X的分布列及数学期望E(X).附表及公式.P(k2≥k)0.150.100.050.0250.0100.0050.001k2.0722.7063.8415.0246.6357.87910.828k2=.19.已知菱形ABCD,AB=2,∠BAD=,半圆O所在平面垂直于平面ABCD,点P在半圆弧上.(不同于B,C).(1)若PA与平面ABCD所成角的正弦值为,求出点P的位置;(2)是否存在点P,使得PC⊥BD,若存在,求出点P的位置,若不存在,说明理由.20.给定椭圆C:+=1(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知点A(2,1)是椭圆G:x2+4y2=m上的点.(1)若过点的直线l与椭圆G有且只有一个公共点,求l被椭圆G的伴随圆G1所截得的弦长;(2)椭圆G上的B,C两点满足4k1•k2=﹣1(其中k1,k2是直线AB,AC的斜率),求证:B,C,O三点共线.21....