广东省广州大学附中高考数学二轮简易通全套课时检测 算法初步与框图 新人教版VIP免费

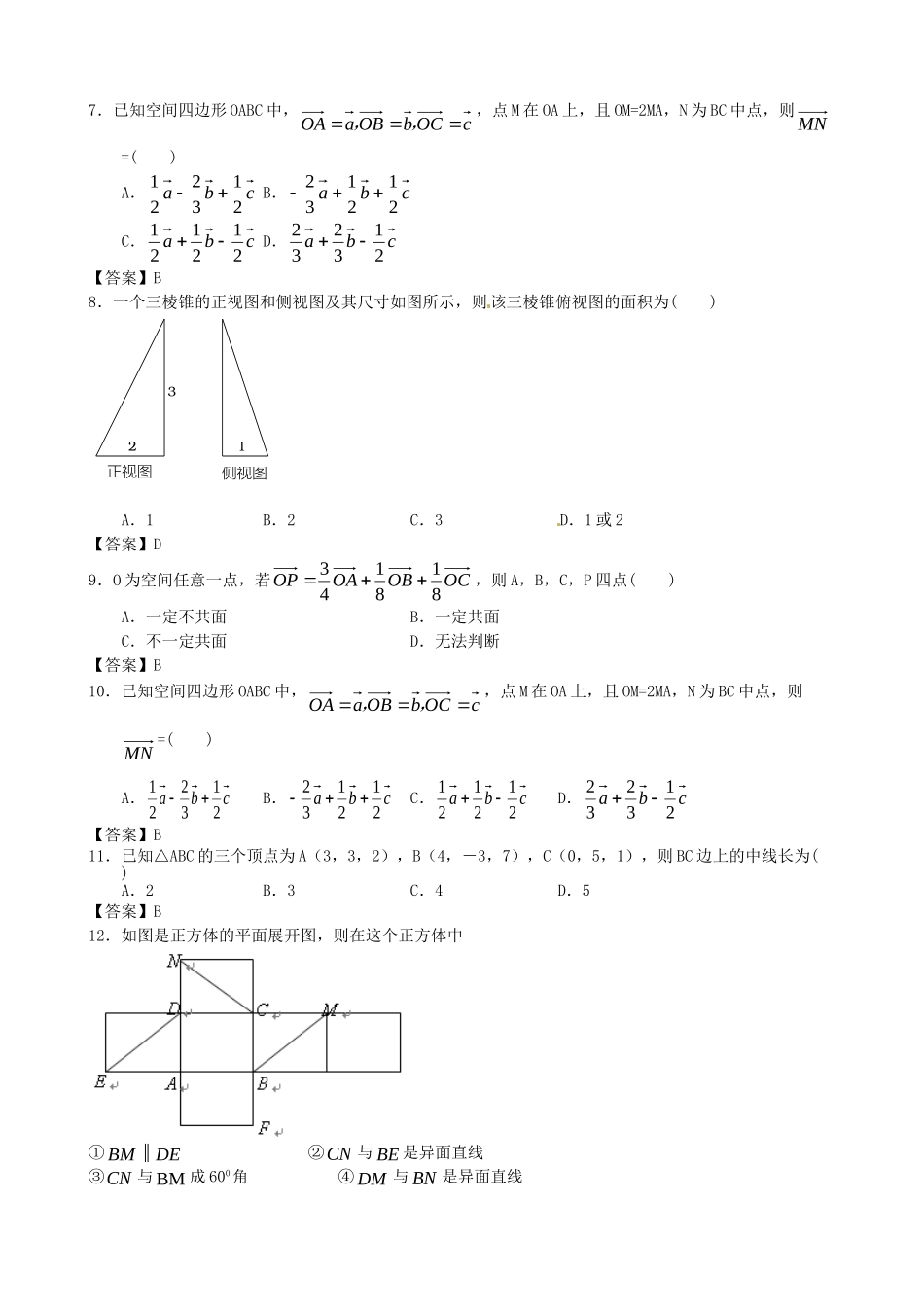
广州大学附中年创新设计高考数学二轮简易通全套课时检测：算法初步与框图本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．点)1,2,3(M关于面yoz对称的点的坐标是()A．)1,2,3(B．)1,2,3(C．)1,2,3(D．)1,2,3(【答案】A2．某几何体的三视图如图所示，则它的体积是()A．283B．83C．82D．23【答案】A3．圆柱的一个底面积为S，侧面展开图是一个正方形，那么这个圆柱的侧面积是()A．SB．S2C．S4D．S332【答案】C4．下面图形中是正方体展开图的是()【答案】A5．下列命题中错误的是()A．如果平面α⊥平面β，那么平面α内一定存在直线平行于平面βB．如果平面α不垂直于平面β，那么平面α内一定不存在直线垂直于平面βC．如果平面α⊥平面γ，平面β⊥平面γ，α∩β＝l，那么l⊥平面γD．如果平面α⊥平面β，那么平面α内所有直线都垂直于平面β【答案】D6．给出下列命题：①有两个面平行，其余各面都是平行四边形所围成的几何体一定是棱柱；②有一个面是多边形，其余各面都是三角形所围成的几何体是棱锥；③用一个平行于棱锥底面的平面去截棱锥，得到的几何体叫棱台.以上命题中真命题的个数为()A．0B．1C．2D．3【答案】A7．已知空间四边形OABC中，cOC，bOB，aOA，点M在OA上，且OM=2MA，N为BC中点，则MN=()A．cba213221B．cba212132C．cba212121D．cba213232【答案】B8．一个三棱锥的正视图和侧视图及其尺寸如图所示，则该三棱锥俯视图的面积为()123侧视图正视图A．1B．2C．3D．1或2【答案】D9．O为空间任意一点，若OCOBOAOP818143，则A，B，C，P四点()A．一定不共面B．一定共面C．不一定共面D．无法判断【答案】B10．已知空间四边形OABC中，cOC，bOB，aOA，点M在OA上，且OM=2MA，N为BC中点，则MN=()A．cba213221B．cba212132C．cba212121D．cba213232【答案】B11．已知△ABC的三个顶点为A（3，3，2），B（4，－3，7），C（0，5，1），则BC边上的中线长为()A．2B．3C．4D．5【答案】B12．如图是正方体的平面展开图，则在这个正方体中①BM∥DE②CN与BE是异面直线③CN与BM成600角④DM与BN是异面直线以上命题中，正确命题的序号是()A．①②③B．②④C．③④D．②③④【答案】C第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上)13．以正方体的顶点为顶点所构成的四棱锥和四面体的个数之差的绝对值是。【答案】1014．给出下列四个命题①平行于同一平面的两条直线平行；②垂直于同一平面的两条直线平行；③如果一条直线和一个平面平行，那么它和这个平面内的任何直线都平行；④如果一条直线和一个平面垂直，那么它和这个平面内的任何直线都垂直．其中正确命题的序号是(写出所有正确命题的序号）．【答案】②④15．在空间直角坐标系Oxyz中，满足条件2221xyz的点(,,)xyz构成的空间区域2的体积为2V（,,xyz分别表示不大于,,xyz的最大整数），则2V=_【答案】816．点1,1,2P关于xoy平面的对称点的坐标是【答案】(1,1,2)三、解答题(本大题共6个小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．如图，在各棱长均为2的三棱柱ABC-A1B1C1中，侧面A1ACC1⊥底面ABC，∠A1AC=60°.(Ⅰ)求侧棱AA1与平面AB1C所成角的正弦值的大小；(Ⅱ)已知点D满足BDBABC�，在直线AA1上是否存在点P，使DP∥平面AB1C？若存在，请确定点P的位置；若不存在，请说明理由.【答案】(Ⅰ) 侧面A1ACC1⊥底面ABC，作A1O⊥AC于点O，∴A1O⊥平面ABC.又∠ABC=∠A1AC=60°，且各棱长都相等，∴AO=1，OA1=OB=3，BO⊥AC.故以O为坐标原点，建立如图所示的空间直角坐标系O-xyz,则A(0，-1，0)，B(3，0，0)，A1(0，0，3)，C(0，1，0)，1(0,1,3)AA�；∴0,2,0,3,2,31ACAB.设平面AB1C的法向量为n=(x,y,1)则023231yACnyxABn解得n=(-1,0,...