高考数学复习点拨 圆的方程---知能聚焦VIP免费

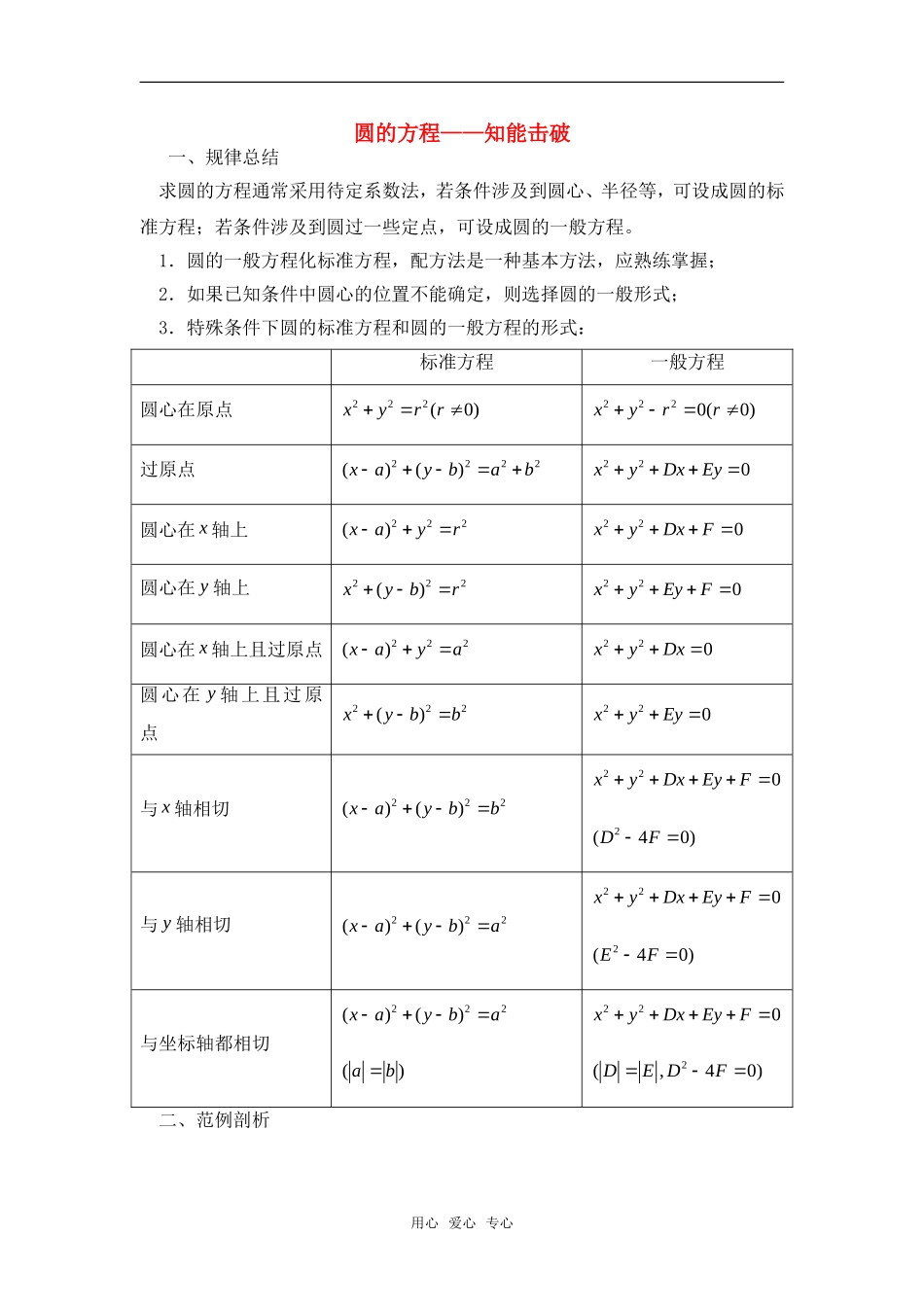
圆的方程——知能击破一、规律总结求圆的方程通常采用待定系数法，若条件涉及到圆心、半径等，可设成圆的标准方程；若条件涉及到圆过一些定点，可设成圆的一般方程。1．圆的一般方程化标准方程，配方法是一种基本方法，应熟练掌握；2．如果已知条件中圆心的位置不能确定，则选择圆的一般形式；3．特殊条件下圆的标准方程和圆的一般方程的形式：标准方程一般方程圆心在原点222(0)xyrr2220(0)xyrr过原点2222()()xaybab220xyDxEy圆心在x轴上222()xayr220xyDxF圆心在y轴上222()xybr220xyEyF圆心在x轴上且过原点222()xaya220xyDx圆心在y轴上且过原点222()xybb220xyEy与x轴相切222()()xaybb220xyDxEyF2(40)DF与y轴相切222()()xayba220xyDxEyF2(40)EF与坐标轴都相切222()()xayba()ab220xyDxEyF2(,40)DEDF二、范例剖析用心爱心专心例1求经过两点(1,4)A，(3,2)B且圆心在y轴上的圆的方程。解析：∵圆心在y轴上，∴0a，设圆的标准方程为222()xybr，∵圆经过A、B两点，∴222222(1)(4)3(2)brbr∴2110br，故圆的方程为22(1)10xy。评注：求圆的标准方程时，要先设出圆的方程，而后用待定系数法求圆心坐标和半径。例2求过原点及(1,1)A且在x轴上截得的线段长为3的圆的方程。分析：有关曲线在坐标轴上截得的线段问题，应考虑曲线在坐标轴上的截距，该例令0y，可得曲线在x轴上的截距1x，2x，从而得到x轴上的线段长度为12xx。解析：依题意，设所求圆的方程为220xyDxEy。令0y，则方程为20xDx，∴10x，2xD，∴123xx，3D，∴3D。又所求圆过点(1,1)A，∴20DE，∴3351DDEE或。故所求圆的方程为22350xyxy或2230xyxy。评注：涉及圆的弦长问题，除利用圆的几何性质外，还可利用一元二次方程的根与系数的关系解决这个问题。本例给出的是解决弦长问题的一般方法。用心爱心专心例3求与x轴切于点(5,0)并在y轴上截取弦长为10的圆的方程。解析：设所求圆的方程为222()()xaybb，圆与x轴切于点(5,0)，∴5a，∵圆在y轴上截得的弦长为10，∴22210()2ab，∴250b，52b。故所求圆的方程为22(5)(52)50xy。评注：根据弦心距、半弦长、半径之间的关系得出22210()2ar是解决问题的关键。用心爱心专心