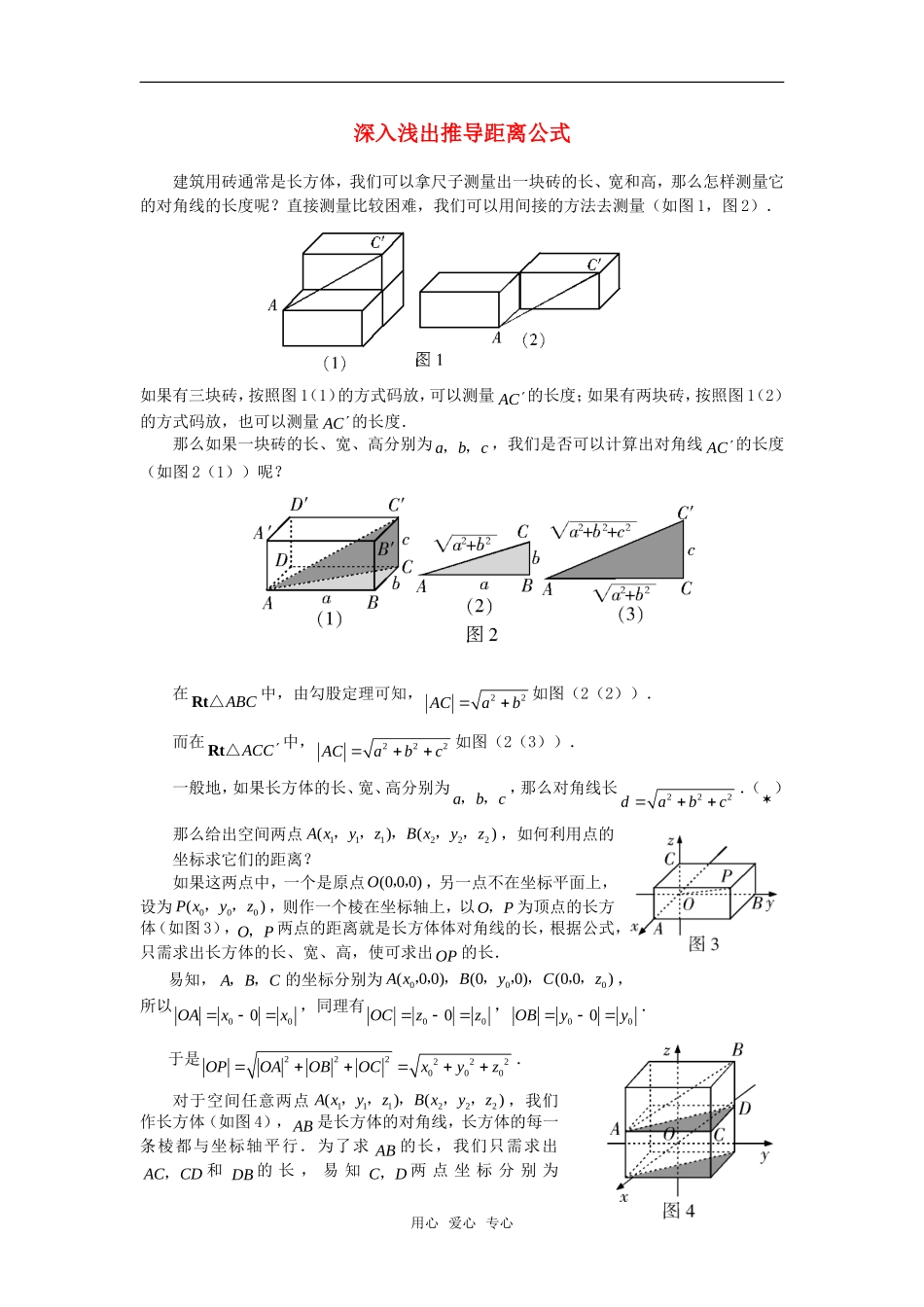
深入浅出推导距离公式建筑用砖通常是长方体,我们可以拿尺子测量出一块砖的长、宽和高,那么怎样测量它的对角线的长度呢?直接测量比较困难,我们可以用间接的方法去测量(如图1,图2).如果有三块砖,按照图1(1)的方式码放,可以测量AC的长度;如果有两块砖,按照图1(2)的方式码放,也可以测量AC的长度.那么如果一块砖的长、宽、高分别为abc,,,我们是否可以计算出对角线AC的长度(如图2(1))呢?在ABCRt△中,由勾股定理可知,22ACab如图(2(2)).而在ACCRt△中,222ACabc如图(2(3)).一般地,如果长方体的长、宽、高分别为abc,,,那么对角线长222dabc.()那么给出空间两点111222()()AxyzBxyz,,,,,,如何利用点的坐标求它们的距离?如果这两点中,一个是原点(000)O,,,另一点不在坐标平面上,设为000()Pxyz,,,则作一个棱在坐标轴上,以OP,为顶点的长方体(如图3),OP,两点的距离就是长方体体对角线的长,根据公式,只需求出长方体的长、宽、高,使可求出OP的长.易知,ABC,,的坐标分别为000(00)(00)(00)AxByCz,,,,,,,,,所以000OAxx,同理有000OCzz,000OByy.于是222222000OPOAOBOCxyz.对于空间任意两点111222()()AxyzBxyz,,,,,,我们作长方体(如图4),AB是长方体的对角线,长方体的每一条棱都与坐标轴平行.为了求AB的长,我们只需求出ACCD,和DB的长,易知CD,两点坐标分别为用心爱心专心121221()()xyzxyz,,,,,由于AC平行于y轴,所以12ACyy,同理有1212CDxxDBzz,.再利用公式(),就有222ABACCDDB,即222121212()()()ABxxyyzz,这就是空间两点间的距离公式.下面我们用所推导的空间两点间的距离公式来做两道题吧!例1求空间两点12(325)(601)PP,,,,,间的距离12PP.解:利用两点间距离公式,得22212(63)[0(2)](15)94367PP.例2平面上到坐标原点的距离为1的点的轨迹是单位圆,其方程为221xy,在空间中,到坐标原点的距离为1的点的轨迹是什么?试写出它的方程.解:与坐标原点的距离为1的点()Pxyz,,的轨迹是一个球面,满足1OP,即2221xyz.因此2221xyz,这就是所求的球面方程.用心爱心专心