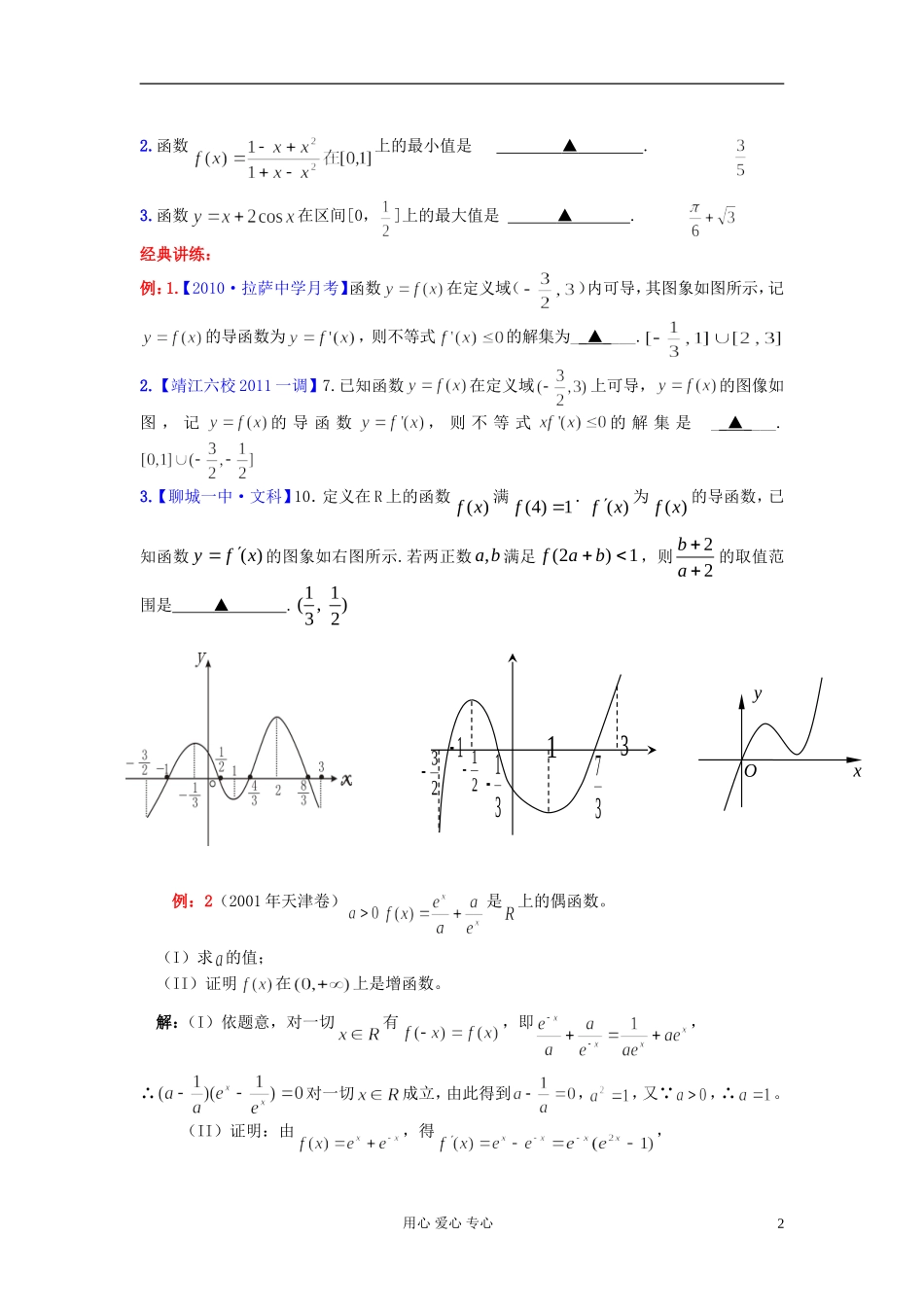
导数与函数单调性一、上节回顾:【临沂高新实验中学】8.将函数xxfysin)(的图象向左平移4个单位,得到函数xy2sin21的图象,则)(xf是▲xsin2二、08~11年江苏数学命题研究及12年走势分析2011年江苏省高考说明中,《导数及其应用》属于必做题部分,其中导数的概念是A级要求,导数的几何意义,导数的运算,利用导数研究函数的单调性与极值,以及导数在实际问题中的应用是B级要求.导数与函数、数列、三角、不等式、解析几何等知识有着密切的联系,导数作为工具在研究函数的性质及在实际生活中有着广泛的应用,导数是高中数学中与高等数学联系最密切的知识之一,所以备受高考命题老师的重视.2008年14题考查导数在函数单调性的综合运用2009年03题考查导数研究函数单调性2010年14题考查导数研究函数性质2011年12题考查指数函数、导数的几何意义导数—导数作为新增内容应为考查的重点内容。利用导数刻划函数,或已知函数性质求参数范围等,2008年江苏考了一道“导数应用题”,理科加试考了“导数与定积分混合型”题,2009年未考大题。那么2011年仍应重视导数题的考查,以中档题为主。小题中两年都考了三次函数,应该更加关注指、对数函数,三角函数的导数及相关的超越函数.三、知识点梳理:函数单调性:⑴函数单调性的判定方法:设函数)(xfy在某个区间内可导,如果)('xf>0,则)(xfy为增函数;如果)('xf<0,则)(xfy为减函数.⑵常数的判定方法;如果函数)(xfy在区间I内恒有)('xf=0,则)(xfy为常数.注:①0)(xf是f(x)递增的充分条件,但不是必要条件,如32xy在),(上并不是都有0)(xf,有一个点例外即x=0时f(x)=0,同样0)(xf是f(x)递减的充分非必要条件.②一般地,如果f(x)在某区间内有限个点处为零,在其余各点均为正(或负),那么f(x)在该区间上仍旧是单调增加(或单调减少)的.经典体验:1.【07广东12】函数()ln(0)fxxxx的单调递增区间是▲.1,e用心爱心专心12.函数上的最小值是▲.3.函数在区间[0,]上的最大值是▲.经典讲练:例:1.【2010·拉萨中学月考】函数在定义域()内可导,其图象如图所示,记的导函数为,则不等式的解集为__▲____.2.【靖江六校2011一调】7.已知函数在定义域上可导,的图像如图,记的导函数,则不等式的解集是__▲____.3.【聊城一中·文科】10.定义在R上的函数)(xf满(4)1f.)(xf为)(xf的导函数,已知函数)(xfy的图象如右图所示.若两正数ba,满足1)2(baf,则22ba的取值范围是▲.11(,)32例:2(2001年天津卷)是上的偶函数。(I)求的值;(II)证明在上是增函数。解:(I)依题意,对一切有,即,∴对一切成立,由此得到,,又 ,∴。(II)证明:由,得,用心爱心专心232112131373xyO当时,有,此时。∴在上是增函数。变式练习1.已知函数.(1)讨论函数()fx的单调性;(2)证明:若5a,则对任意2,有1212()()1fxfxxx.解:(1)()fx的定义域为(0,),2'11(1)(1)()axaxaxxafxxaxxx(i)若11a即2a,则2'(1)()xfxx故()fx在(0,)单调增加.(ii)若11a,而1a,故12a,则当(1,1)xa时,'()0fx.当(0,1)xa及(1,)x时,'()0fx,故()fx在(1,1)a单调减少,在(0,1),(1,)a单调增加.(iii)若11a,即2a,同理可得()fx在(1,1)a单调减少,在(0,1),(1,)a单调增加.(2)考虑函数()()gxfxx21(1)ln2xaxaxx则,由于,故()0gx,即在单调增加,从而当120xx时有12()()0gxgx,即1212()()0fxfxxx,故1212()()1fxfxxx,当120xx时,用心爱心专心3有12211221()()()()1fxfxfxfxxxxx.变式练习2求下列函数的最值.1.;2.,例:3【2010黄冈中学】若函数在其定义域内的一个子区间内不是单调函数,则实数k的取值范围是▲.【解析】因为定义域为,,由,得.据题意,,解得变式练习1【温州十校联合·理】22已知函数21()ln(4)2fxxxax(1,)在上是增函数.(I)求实数a的取值范围;【解】(I).41)(axxxf.2)1(4),,1(21.)1(4,),1(041,),1()(...