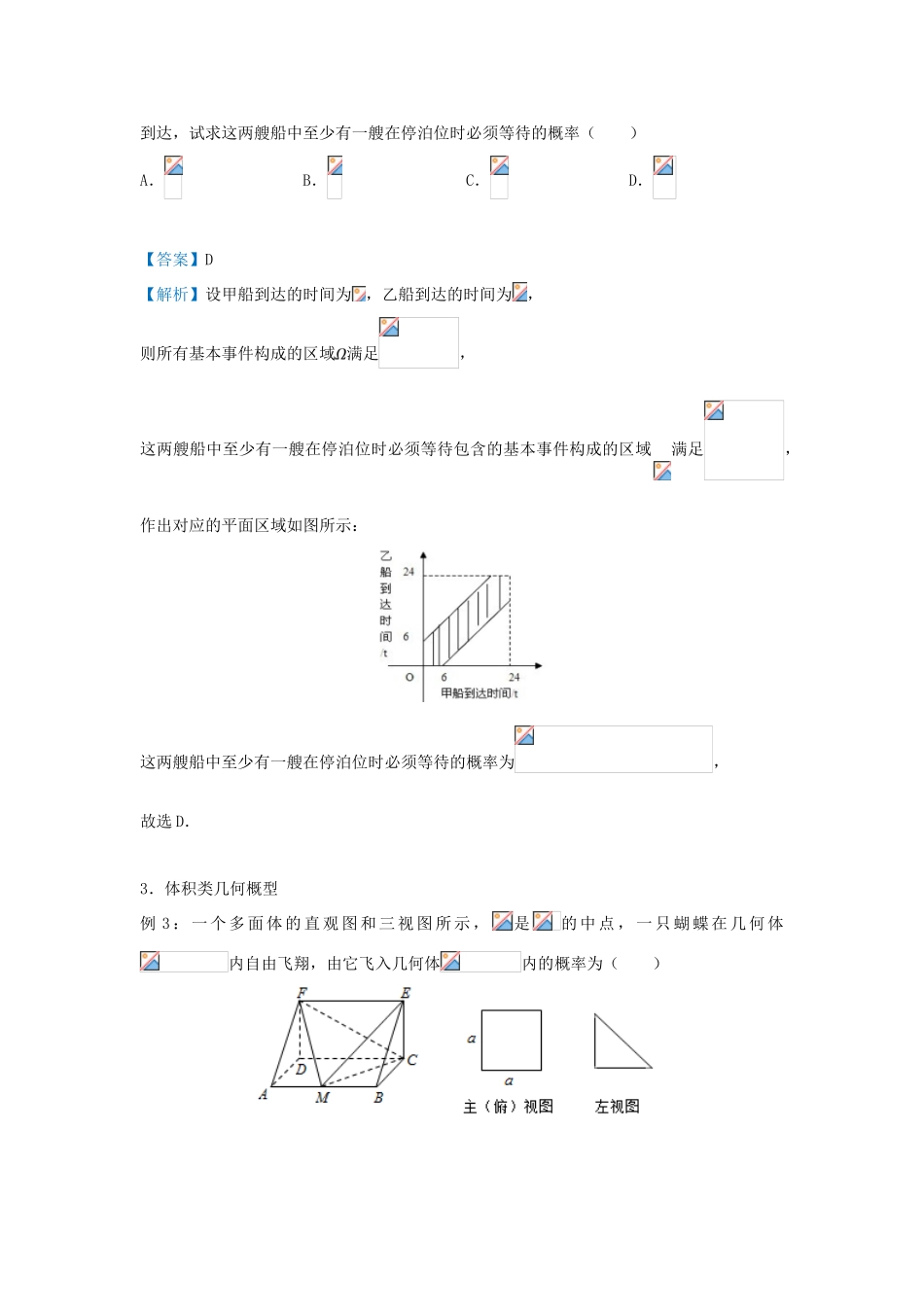
培优点十九几何概型1.长度类几何概型例1:已知函数,,在定义域内任取一点,使的概率是()A.B.C.D.【答案】C【解析】先解出时的取值范围:,从而在数轴上区间长度占区间长度的比例即为事件发生的概率,∴,故选C.2.面积类几何概型(1)图形类几何概型例2-1:如图所示,在矩形中,,,图中阴影部分是以为直径的半圆,现在向矩形内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是()A.1000B.2000C.3000D.4000【答案】C【解析】在矩形中,,,面积为,半圆的面积为,故由几何概型可知,半圆所占比例为,随机撒4000粒豆子,落在阴影部分内的豆子数目大约为3000,故选C.(2)线性规划类几何概型例2-2:甲乙两艘轮船都要在某个泊位停靠6小时,假定他们在一昼夜的时间段中随机地到达,试求这两艘船中至少有一艘在停泊位时必须等待的概率()A.B.C.D.【答案】D【解析】设甲船到达的时间为,乙船到达的时间为,则所有基本事件构成的区域满足,这两艘船中至少有一艘在停泊位时必须等待包含的基本事件构成的区域满足,作出对应的平面区域如图所示:这两艘船中至少有一艘在停泊位时必须等待的概率为,故选D.3.体积类几何概型例3:一个多面体的直观图和三视图所示,是的中点,一只蝴蝶在几何体内自由飞翔,由它飞入几何体内的概率为()A.B.C.D.【答案】D【解析】所求概率为棱锥的体积与棱柱体积的比值.由三视图可得,且,,两两垂直,可得,棱锥体积,而,∴.从而.故选D.一、单选题1.如图,边长为2的正方形中有一阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为.则阴影区域的面积约为()A.B.C.D.无法计算【答案】C对点增分集训【解析】设阴影区域的面积为,,∴.故选C.2.某景区在开放时间内,每个整点时会有一趟观光车从景区入口发车,某人上午到达景区入口,准备乘坐观光车,则他等待时间不多于10分钟的概率为()A.B.C.D.【答案】B【解析】由题意,此人在50分到整点之间的10分钟内到达,等待时间不多于10分钟,∴概率.故选B.3.一只蚂蚁在边长为4的正三角形区域内随机爬行,则它在离三个顶点距离都大于2的区域内的概率为()A.B.C.D.【答案】A【解析】满足条件的正三角形如图所示:其中正三角形的面积满足到正三角形的顶点,,的距离都小于2的平面区域如图中阴影部分所示,则,则使取到的点到三个顶点,,的距离都大于2的概率为:.故选A.4.在区间上随机取两个数,,记为事件的概率,则()A.B.C.D.【答案】D【解析】如图所示,,表示的平面区域为,平面区域内满足的部分为阴影部分的区域,其中,,结合几何概型计算公式可得满足题意的概率值为,故选D.5.在区间上随机取一个数,的值介于0到之间的概率为()A.B.C.D.【答案】A【解析】由,得,或,∴或,记的值介于0到之间,则构成事件的区域长度为;全部结果的区域长度为2;∴,故选A.6.点在边长为1的正方形内运动,则动点到定点的距离的概率为()A.B.C.D.【答案】C【解析】满足条件的正方形,如图所示:其中满足动点到定点的距离的平面区域如图中阴影部分所示,则正方形的面积,阴影部分的面积.故动点到定点的距离的概率.故选C.7.已知实数,执行如图所示的程序框图,则输出的不小于103的概率为()A.B.C.D.【答案】B【解析】设实数,经过第一次循环得到,;经过第二次循环得到,;经过第三次循环得到,,此时输出,输出的值为,令得,由几何概型概率得到输出的不小于103的概率为,故选B.8.《九章算术》中有如下问题:“今有勾五步,股一十二步,问勾中容圆,径几何?”其大意:“已知直角三角形两直角边分别为5步和12步,问其内切圆的直径为多少步?”现若向此三角形内随机投一粒豆子,则豆子落在其内切圆外的概率是()A.B.C.D.【答案】C【解析】直角三角形的斜边长为,设内切圆的半径为,则,解得,∴内切圆的面积为,∴豆子落在其内切圆外部的概率是,故选C.9.把不超过实数的最大整数记为,则函数称作取整函数,又叫高斯函数,在上任取,则的概率为()A.B....