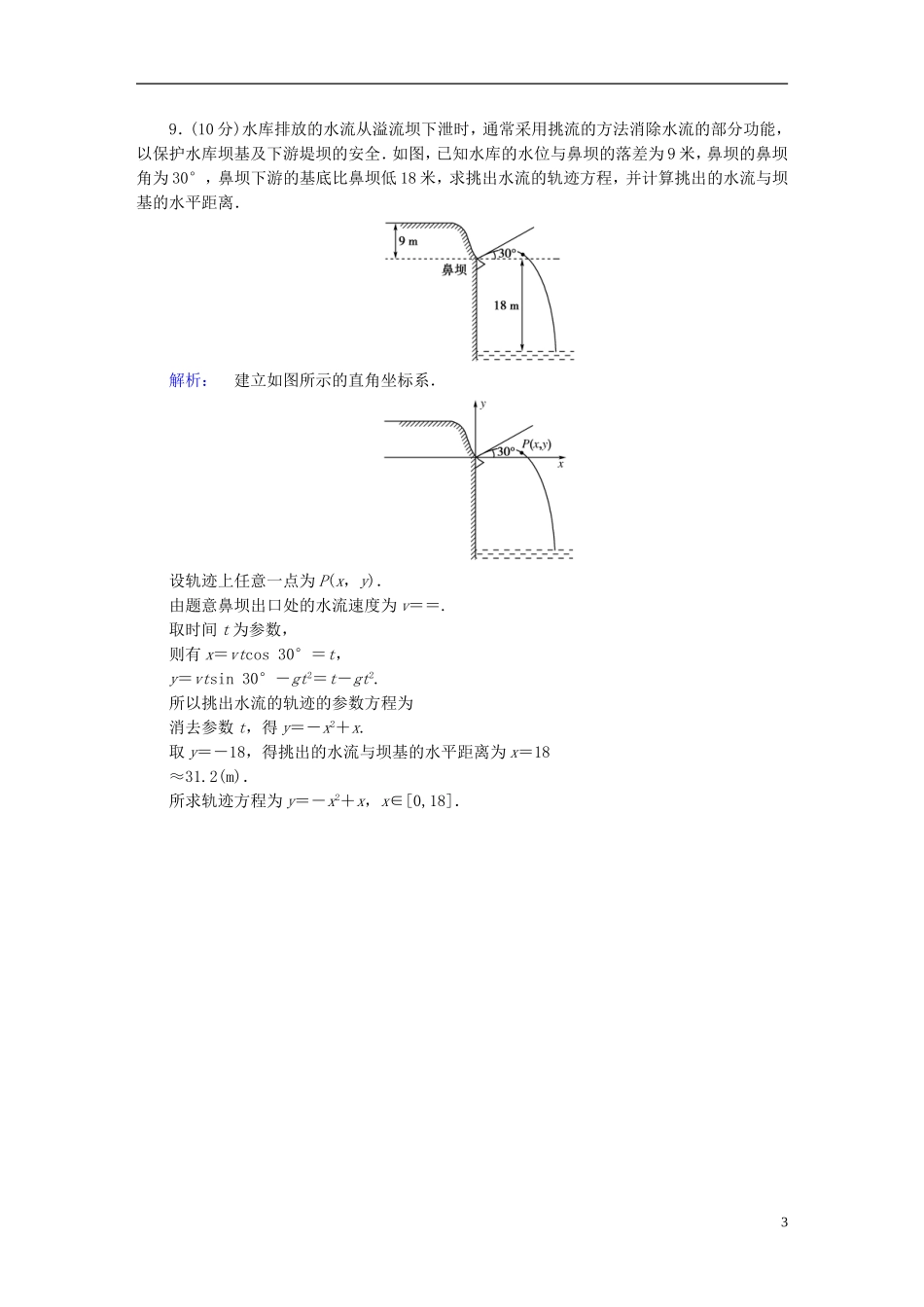
2016-2017学年高中数学第2讲参数方程2圆锥曲线的参数方程课后练习新人教A版选修4-4一、选择题(每小题5分,共20分)1.θ取一切实数时,连接A(4sinθ,6cosθ)和B(-4cosθ,6sinθ)两点的线段的中点轨迹是()A.圆B.椭圆C.直线D.线段解析:设中点M(x,y),由中点坐标公式,得x=2sinθ-2cosθ,y=3cosθ+3sinθ,即=sinθ-cosθ,=sinθ+cosθ,两式平方相加,得+=2,是椭圆.答案:B2.参数方程(0≤θ<2π)表示轨迹()A.双曲线的一支,过点B.抛物线的一部分,过点C.双曲线的一支,过点D.抛物线的一部分,过点解析:因为x2=1+sinθ,所以x2=2y表示抛物线,又因为x==∴x∈[0,],是抛物线的一部分.且当θ=π时,有x=1,y=,即曲线过点.答案:B3.下列参数方程(t为参数)与普通方程x2-y=0表示同一曲线的方程是()A.B.C.D.解析:注意参数范围,可利用排除法.普通方程x2-y=0中的x∈R,y≥0.A中x=|t|≥0,B中x=cost∈[-1,1],故排除A和B.而C中y==cot2t==,即x2y=1,故排除C.答案:D4.已知过曲线(θ为参数,0≤θ≤π)上一点P,原点为O,直线PO的倾斜角为,则P点坐标是()A.(3,4)B.C.(-3,-4)D.解析:设|OP|=t,则P点坐标,代入方程+=1,解得t=,所以P点坐标.答案:D二、填空题(每小题5分,共10分)5.设椭圆的参数方程为(0≤θ≤π),M(x1,y1),N(x2,y2)是椭圆上两点.M,N对应的参数为θ1,θ2且x1θ2.答案:θ1>θ26.已知抛物线y2=2px(p>0),过顶点的两弦OA⊥OB,则分别以OA,OB为直径的两圆的另一交点Q的轨迹是________.解析:设A(2pt,2pt1),B(2pt,2pt2),则以OA为直径的圆的方程为x2+y2-2ptx-2pt1y=0,以OB为直径的圆的方程为x2+y2-2ptx-2pt2y=0,即t1,t2为方程2pxt2+2pyt-x2-y2=0的两根,∴t1t2=.又OA⊥OB,∴t1t2=-1,即x2+y2-2px=0,∴另一交点Q的轨迹是以(p,0)为圆心,p为半径的圆.答案:以(p,0)为圆心,p为半径的圆三、解答题(每小题10分,共20分)7.如图所示,已知曲线4x2+9y2=36(x>0,y>0),点A在曲线上移动,点C(6,4),以AC为对角线作矩形ABCD,使AB∥x轴,AD∥y轴,求矩形ABCD的面积最小时点A坐标.解析:∵椭圆方程为+=1,设A(3cosθ,2sinθ),θ∈,则B(6,2sinθ),C(6,4),D(3cosθ,4),∴SABCD=|AB|·|AD|=(6-3cosθ)·(4-2sinθ)=24-12(sinθ+cosθ)+6sinθcosθ,令t=sinθ+cosθ,则t∈(1,],sinθcosθ=,则SABCD=3(t-2)2+9.因为t∈(1,],所以,当t=时,矩形面积最小,即t=sinθ+cosθ=sin=,此时,θ=.所以矩形ABCD的面积最小时点A坐标是.8.直线l:x+2y-6=0与抛物线y2=2x交于A、B两点,求∠AOB的值.解析:设抛物线y2=2x的参数方程是(t是参数),将它代入直线l的方程x+2y-6=0,整理得3t2+2t-3=0①∵A、B对应的参数t1,t2分别是方程①的两根,∴t1·t2=-1.∵t表示的是抛物线上除原点外的任一点与原点连线斜率的倒数,∴·=-1,即kOA·kOB=-1,∴∠AOB=90°.29.(10分)水库排放的水流从溢流坝下泄时,通常采用挑流的方法消除水流的部分功能,以保护水库坝基及下游堤坝的安全.如图,已知水库的水位与鼻坝的落差为9米,鼻坝的鼻坝角为30°,鼻坝下游的基底比鼻坝低18米,求挑出水流的轨迹方程,并计算挑出的水流与坝基的水平距离.解析:建立如图所示的直角坐标系.设轨迹上任意一点为P(x,y).由题意鼻坝出口处的水流速度为v==.取时间t为参数,则有x=vtcos30°=t,y=vtsin30°-gt2=t-gt2.所以挑出水流的轨迹的参数方程为消去参数t,得y=-x2+x.取y=-18,得挑出的水流与坝基的水平距离为x=18≈31.2(m).所求轨迹方程为y=-x2+x,x∈[0,18].3