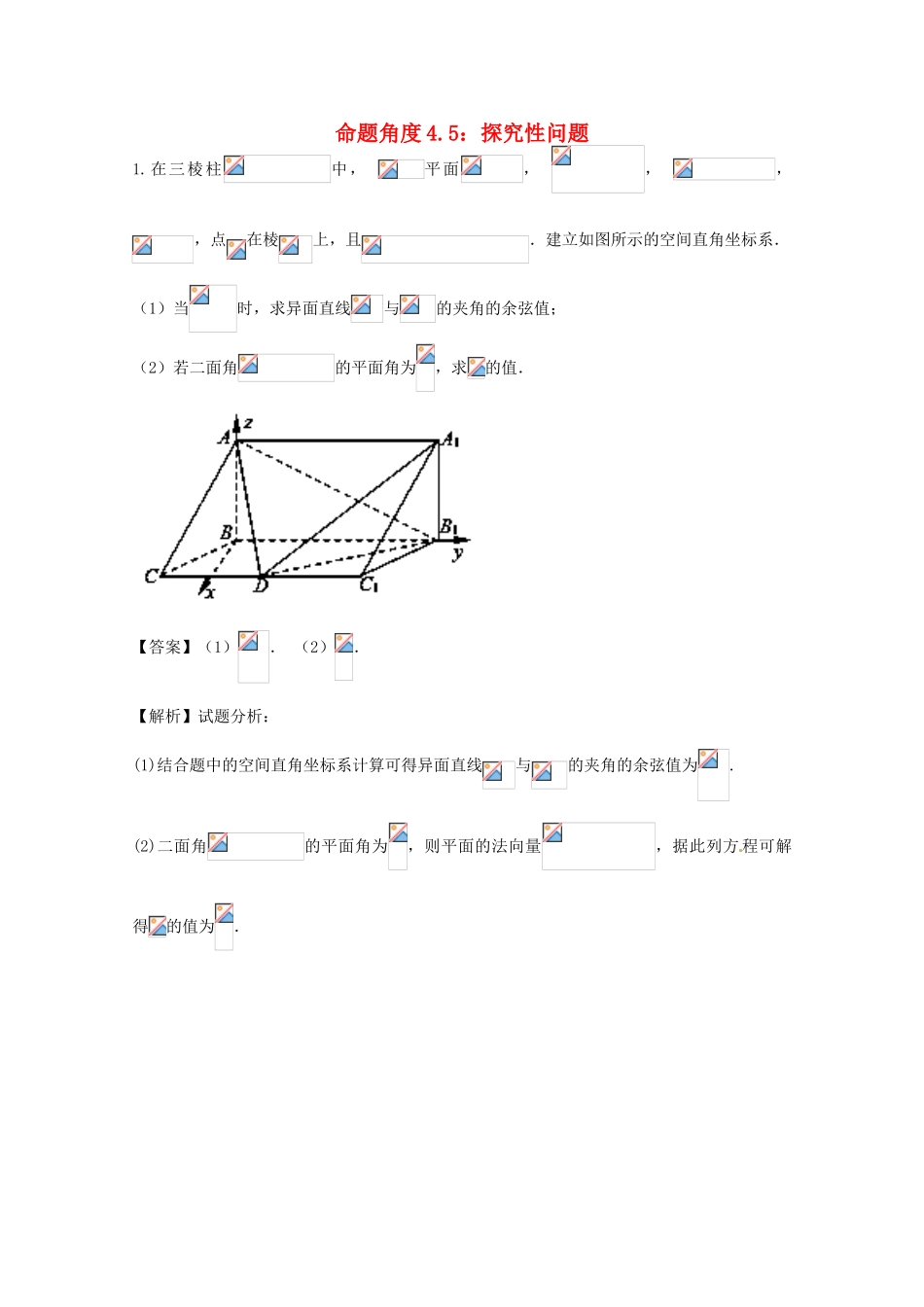
命题角度4.5:探究性问题1.在三棱柱中,平面,,,,点在棱上,且.建立如图所示的空间直角坐标系.(1)当时,求异面直线与的夹角的余弦值;(2)若二面角的平面角为,求的值.【答案】(1).(2).【解析】试题分析:(1)结合题中的空间直角坐标系计算可得异面直线与的夹角的余弦值为.(2)二面角的平面角为,则平面的法向量,据此列方程可解得的值为..故异面直线与的夹角的余弦值为.设平面的法向量为,则即令,解得,,所以平面的一个法向量为.因为二面角的平面角为,所以,即,解得或(舍),故的值为.点睛:立体几何开放性问题求解方法有以下两种:(1)根据题目的已知条件进行综合分析和观察猜想,找出点或线的位置,然后再加以证明,得出结论;(2)假设所求的点或线存在,并设定参数表达已知条件,根据题目进行求解,若能求出参数的值且符合已知限定的范围,则存在这样的点或线,否则不存在.2.如图,在四棱锥中,底面为平行四边形,,,底面.(1)求证:平面平面;(2)在棱上是否存在一点,使得二面角的平面角的余弦值为?若存在,求出的值?若不存在,说明理由.【答案】(1)见解析;(2)λ=.【解析】试题分析:(1)由线面垂直的性质,勾股定理分别可得、,从而得平面,进而可得结果;(2)以为原点所在直线分别为x、轴,轴,轴建立如图所示坐标系,分别求出平面与平面的一个法向量,根据空间向量夹角余弦公式,可得结果.试题解析:(1)在ACD中,AC=a,CD=a,AD=a由勾股定理得:CD⊥AC PA⊥底面ABCD∴PA⊥CDAC面PAC,PA面PAC,PA∩AC=A∴CD⊥面PAC又 CD面PCD∴平面PCD⊥平面PAC.(2)由(1)知:AB⊥AC,又PA⊥底面ABCD∴以A为原点AB,AC,AP所在直线分别为x轴,y轴,z轴建立如图所示坐标系则A(0,0,0),B(a,0,0),C(0,a,0),D(-a,a,0),P(0,0,a)假设点E存在,且λ=,则=λ(xE,yE-a,zE)=λ(0,-a,a)∴xE=0,yE=(1-λ)a,zE=λa=(a,0,0)=(0,(1-λ)a,λa),=(-a,a,0)设平面BAE的法向量为=(x1,y1,z1),平面DAE的法向量为=(x2,y2,z2),则=(0,λ,λ-1)=(λ,λ,λ-1)cos<,>====由题意:|cos<,>|=即:=3(2λ2-2λ+1)=2(3λ2-2λ+1)∴λ=∴棱PC上存在一点E,使得二面角B-AE-D的平面角的余弦值为-,且此时λ=.【方法点晴】本题主要考查利用空间向量求法向量以及面面垂直的判定定理,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.3.如图,在棱长为2的正方体中,,,,分别是棱,,,的中点,点,分别在棱,上移动,且.(1)当时,证明:直线平面;(2)是否存在,使面与面所成的二面角为直二面角?若存在,求出的值;若不存在,说明理由.【答案】(1)见解析;(2).(2)设平面的一个法向量为,则由,得,于是可取.设平面的一个法向量为,由,得,于是可取.若存在,使面与面所成的二面角为直二面角,则,即,解得,显然满足.故存在,使面与面所成的二面角为直二面角.点睛:立体几何的有关证明题,首先要熟悉各种证明的判定定理,然后在进行证明,要多总结题型,对于二面角问题一般直接建立空间直角坐标系,求出法向量然后根据向量夹角公式求解二面角,要注意每一个坐标的准确性4.如图,在四棱锥中,,平面,.(1)设点为的中点,求证:平面;(2)线段上是否存在一点,使得直线与平面所成的角的正弦值为?若存在,试确定点的位置;若不存在,请说明理由.【答案】(1)见解析(2)为中点【解析】试题分析:(1)先取的中点,利用三角形中位线性质得,再根据线面平行判定定理得平面.根据计算,利用平几知识得,再根据线面平行判定定理得平面.从而利用面面平行判定定理得平面平面.最后根据面面平行性质得平面.(2)一般利用空间直角坐标系研究线面角,先根据条件建立恰当直角坐标系,设立各点坐标,利用方程组求出平面法向量,根据向量数量积求出向量夹角,最后利用线面角与向量夹角关系列方程,解出点坐标,确定其位置.试题解析:(1)证明取的中点,连接,则....